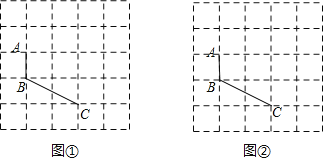题目内容
【题目】如图①,在△ABC中,∠C=90°,AC=8cm,BC=6cm.动点P在线段AC上以5cm/s的速度从点A运动到点C.过点P作PD⊥AB于点D,将△APD绕PD的中点旋转180°得到△A'DP.设点P的运动时间为x(s).
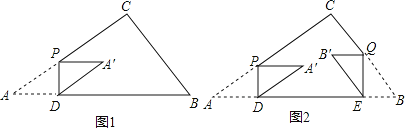
(1)求点A'落在边BC上时x的值.
(2)设△A'DP和△ABC重叠部分图形周长为y(cm),求y与x之间的函数关系式.
(3)如图②,另有一动点Q与点P同时出发,在线段BC上以5cm/s的速度从点B运动到点C.过点Q作QE⊥AB于点E,将△BQE绕QE的中点旋转180°得到△B'EQ.连结A′B′.当直线A'B'与△ABC的边垂直或平行时,直接写出x的值.
【答案】(1)x=![]() ;(2)y=12x(0<x≤
;(2)y=12x(0<x≤![]() ),y=-
),y=-![]() x+12(
x+12(![]() <x≤
<x≤![]() );(3)x=
);(3)x=![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)利用锐角三角函数的意义直接求出;
(2)由(1)计算可得,分两种情况用锐角三角函数的意义求解:①当0<x≤![]() 时,y=12x,当
时,y=12x,当![]() <x≤
<x≤![]() 时,y=12-
时,y=12-![]() x;
x;
(3)分四种情形画出图形分别求解即可解决问题.
解:(1)如图1,
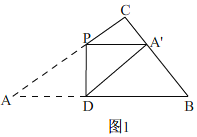
∵∠C=90°,AC=8厘米,BC=6厘米,
∴AB=10(cm),
∴cosA=![]() ,sinA=
,sinA=![]() ,tanA=
,tanA=![]() ,
,
设AP=5x,
∴PA′=AD=APcos∠A=![]() ×5x=4x,CP=8-5x,
×5x=4x,CP=8-5x,
∴cos∠CPA′=cos∠A=![]() =
=![]() =
=![]() ,
,
∴x=![]() ,
,
(2)①当0<x≤![]() ,如图2,
,如图2,
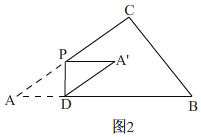
∴PA′=AD=APcosA=3x,
∴A′D=AP=5x,
∴y=4x+3x+5x=12x,
②当![]() <x≤
<x≤![]() 时,如图3
时,如图3
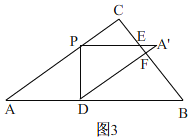
∴PE=![]() =
=![]() =
=![]() ,
,
DF=DB×cosA=8-![]() x,
x,
∴y=3x+![]() +8-
+8-![]() x+
x+![]() x-6=12-
x-6=12-![]() x,
x,
即:当0<x≤![]() 时,y=12x,
时,y=12x,
当![]() <x≤
<x≤![]() 时,y=-
时,y=-![]() x+12;
x+12;
(3)同(1)一样有,sinB=![]() ,cosB=
,cosB=![]() ,tanB=
,tanB=![]() ,
,
①当A′B′⊥AB时,如图6,
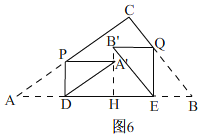
∴DH=PA'=AD=4x,HE=B′Q=EB=3x,
∵AB=2AD+2EB=2×4x+2×3x=10,
∴x=![]() ,
,
∴A′B′=QE-PD=4x-3x=x=![]() .
.
②当A′B′⊥BC时,如图7,
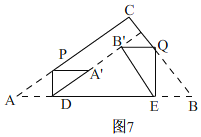
∴B′E=5x,DE=10-7x,
∴cosB=![]() =
=![]() ,
,
∴x=![]() .
.
③当A′B′⊥AC时,如图8,
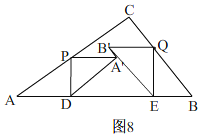
DA'=PA=5x,DE=![]() ×5x=
×5x=![]() x,
x,
∴4x+![]() x+3x=10,
x+3x=10,
∴x=![]() .
.
④当Q,P都到达C后,如图9,
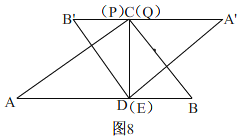
∵A′B′∥AB且AB=A′B′=10,
此时x=![]() s.
s.