题目内容
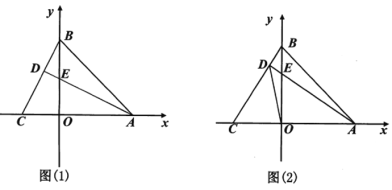
【题目】在平面直角坐标系中,点A(4,0),B(0,4),点C是x轴负半轴上的一动点,连接BC,过点A作直线BC的垂线,垂足为D,交y轴于点E.
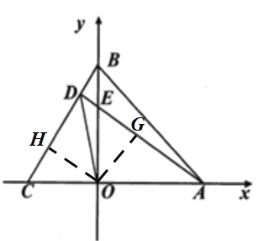
(1)如图(1),
①判断![]() 与
与![]() 是否相等(直接写出结论,不需要证明).
是否相等(直接写出结论,不需要证明).
②若OC=2,求点E的坐标.
(2)如图(2),若OC<4,连接DO,求证:DO平分![]() .
.
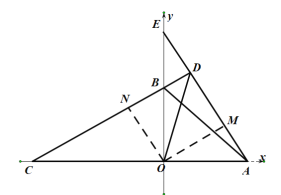
(3)若OC>4时,请问(2)的结论是否成立?若成立,画出图形,并证明;若不成立,说明理由.
【答案】(1)①![]() ,理由见详解;②
,理由见详解;② ![]() (2)见详解;(3)结论依然成立,理由见详解
(2)见详解;(3)结论依然成立,理由见详解
【解析】
(1)①通过![]() 得出
得出![]() ,再通过等量代换即可得出
,再通过等量代换即可得出![]() ;
;
②通过AAS证明![]() ,得出
,得出![]() ,从而可确定点E的坐标;
,从而可确定点E的坐标;
(2)过点O分别作OG⊥AE于点G,OH⊥BC于点H,通过![]() 得出
得出![]() ,从而得出
,从而得出![]() ,最后利用角平分线性质定理的逆定理即可得出结论;
,最后利用角平分线性质定理的逆定理即可得出结论;
(3)过点O分别作OM⊥AE于点G,ON⊥CB于BC于点H,先证明![]() ,通过
,通过![]() 得出
得出![]() ,从而得出
,从而得出![]() ,最后利用角平分线性质定理的逆定理即可得出结论.
,最后利用角平分线性质定理的逆定理即可得出结论.
(1)①![]() ,理由如下:
,理由如下:
![]()
![]()
![]()
![]()
![]()
② ![]()
![]()
在![]() 和
和![]() 中,
中,
![]()
![]()
![]()
![]()
![]()
(2)过点O分别作OG⊥AE于点G,OH⊥BC于点H
![]()
![]()
![]()
![]()
∵OG⊥AE,OH⊥BC
∴点O在![]() 的平分线上
的平分线上
∴DO平分![]()
(3)结论依然成立,理由如下:
过点O分别作OM⊥AE于点G,ON⊥CB于BC于点H
![]()
![]()
![]()
![]()
![]()
![]()
![]()
在![]() 和
和![]() 中,
中,
![]()
![]()
![]()
![]()
∵OM⊥AE,ON⊥BC
∴点O在![]() 的平分线上
的平分线上
∴DO平分![]()

练习册系列答案
相关题目