题目内容
【题目】![]() 是一张等腰直角三角形纸板,
是一张等腰直角三角形纸板,![]() ,
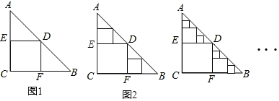
,![]() ,在这张纸板中剪出一个尽可能大的正方形称为第
,在这张纸板中剪出一个尽可能大的正方形称为第![]() 次剪取;在余下的
次剪取;在余下的![]() 和
和![]() 中,分别剪取正方形,得到两个相同的正方形,称为第
中,分别剪取正方形,得到两个相同的正方形,称为第![]() 次剪取(如图
次剪取(如图![]() );继续操作下去…;第
);继续操作下去…;第![]() 次剪取后,余下的所有小三角形的面积之和是________.
次剪取后,余下的所有小三角形的面积之和是________.
【答案】![]()
【解析】
根据题意,可求得S△AED+S△DBF=S正方形ECFD=S1=4,同理可得规律:Sn即是第n次剪取后剩余三角形面积和,根据此规律求解即可答案.
∵四边形ECFD是正方形,
∴DE=EC=CF=DF,∠AED=∠DFB=90°,
∵△ABC是等腰直角三角形,
∴∠A=∠B=45°,
∴AE=DE=EC=DF=BF=EC=CF,
∵AC=BC=4,
∴DE=DF=2,
∴S△AED+S△DBF=S正方形ECFD=S1=4,
同理:S2即是第二次剪取后剩余三角形面积和,Sn即是第n次剪取后剩余三角形面积和,
∴第一次剪取后剩余三角形面积和为:8-S1=4=22=S1,
第二次剪取后剩余三角形面积和为:S1-S2=4-2=21=S2,
第三次剪取后剩余三角形面积和为:S2-S3=20=S3,
…
第n次剪取后剩余三角形面积和为:Sn-1-Sn=Sn=![]() ,
,
故第64次剪取后,余下的所有小三角形的面积之和是:![]() .
.
故答案为:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目