题目内容
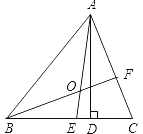
【题目】如图所示，在△ABC中，AE、BF是角平分线，它们相交于点O，AD是高，∠BAC=80°，∠C=54°，求∠DAC、∠BOA的度数．
【答案】∠DAC=36°；∠BOA=117°
【解析】
首先利用AD是高，求得∠ADC，进一步求得∠DAC度数可求；利用三角形的内角和求得∠ABC，再由BF是∠ABC的角平分线，求得∠ABO，故∠BOA的度数可求．
解：∵AD是高
∴∠ADC=90°
∵∠C=54°
∴∠DAC=180°﹣90°﹣54°=36°
∵∠BAC=80°，∠C=54°，AE是角平分线
∴∠BAO=40°，∠ABC=46°
∵BF是∠ABC的角平分线
∴∠ABO=23°
∴∠BOA=180°﹣∠BAO﹣∠ABO=117°
练习册系列答案
名师伴你成长课时同步学练测系列答案
相关题目
