题目内容
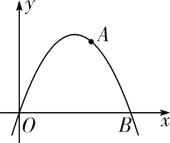
【题目】已知二次函数的解析式为y=-x2+4x,该二次函数交x轴于O、B两点,A为抛物线上一点,且横纵坐标相等(原点除外),P为二次函数上一动点,过P作x轴垂线,垂足为D(a,0)(a>0),并与直线OA交于点C.
(1)求A、B两点的坐标;
(2)当点P在线段OA上方时,过P作x轴的平行线与线段OA相交于点E,求△PCE周长的最大值及此时P点的坐标;
(3)当PC=CO时,求P点坐标.
【答案】(1)B (4,0),A (3,3); (2)△PCE周长的最大值为4+2![]() ,P (1,3);(3)P点坐标为(3-
,P (1,3);(3)P点坐标为(3-![]() ,1+2
,1+2![]() )或(3+
)或(3+![]() ,1-2
,1-2![]() ).
).
【解析】
(1)令y=0,得-x2+4x=0,解方程即可得到点B的坐标,设点A坐标为(x,x),把A(x,x)代入y=-x2+4x中得:x=-x2+4x,解方程即可得出点A的坐标;
(2)根据题意画出图形,设点P的坐标为(x,-x2+4x),再求得PC=-x2+3x,由等腰三角形的性质得,当PC取最大值时,△PCE周长最大,进而求得当x=1时,PC最大,PC的最大值为-1+3=2,从而得出△PCE周长的最大值及此时P点的坐标;
(3)当点P在点C上方时和当点P在点C下方时分别讨论分析.
解:(1)令y=0,则-x2+4x=0,
解得x1=0,x2=4.
∴点B坐标为(4,0),
设点A坐标为(x,x),把A(x,x)代入y=-x2+4x得,
x=-x2+4x,
解得x1=3,x2=0(舍去),
∴点A的坐标为(3,3);
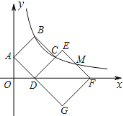
(2)如图,设点P的坐标为(x,-x2+4x),
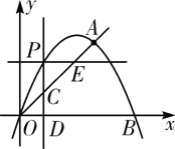
∵点A坐标为(3,3);
∴∠AOB=45°,
∴OD=CD=x,
∴PC=PD-CD=-x2+4x-x=-x2+3x,
∵PE∥x轴,
∴△PCE是等腰直角三角形,
∴当PC取最大值时,△PCE周长最大.
∵PE与线段OA相交,
∴0≤x≤1,
由PC=-x2+3x=-(x-![]() )2+
)2+![]() 可知,抛物线的对称轴为直线x=
可知,抛物线的对称轴为直线x=![]() ,且在对称轴左侧PC随x的增大而增大,
,且在对称轴左侧PC随x的增大而增大,
∴当x=1时,PC最大,PC的最大值为-1+3=2,
∴PE=2,CE=2![]() ,
,
∴△PCE的周长为CP+PE+CE=4+2![]() ,
,
∴△PCE周长的最大值为4+2![]() ,
,
把x=1代入y=-x2+4x,得y=-1+4=3,
∴点P的坐标为(1,3);
(3)设点P坐标为(x,-x2+4x),则点C坐标为(x,x),如解图,

①当点P在点C上方时,P1C1=-x2+4x-x=-x2+3x,OC1=![]() x,
x,
∵P1C1=OC1,
∴-x2+3x=![]() x,
x,
解得x1=3-![]() ,x2=0(舍去).
,x2=0(舍去).
把x=3-![]() 代入y=-x2+4x得,
代入y=-x2+4x得,
y=-(3-![]() )2+4(3-
)2+4(3-![]() )=1+2
)=1+2![]() ,
,
∴P1(3-![]() ,1+2
,1+2![]() ),
),
②当点P在点C下方时,P2C2=x-(-x2+4x)=x2-3x,OC2=![]() x,
x,
∵P2C2=OC2,
∴x2-3x=![]() x,
x,
解得x1=3+![]() ,x2=0(舍去),
,x2=0(舍去),
把x=3+![]() 代入y=-x2+4x,
代入y=-x2+4x,
得y=-(3+![]() )2+4(3+
)2+4(3+![]() )=1-2
)=1-2![]() ,
,
∴P2(3+![]() ,1-2
,1-2![]() ).
).
综上所述,P点坐标为(3-![]() ,1+2
,1+2![]() )或(3+
)或(3+![]() ,1-2
,1-2![]() ).
).

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案