题目内容
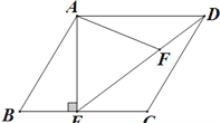
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为( ).
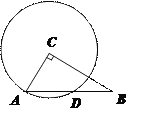
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】分析:先根据勾股定理求出AB的长,过C作CM⊥AB,交AB于点M,由垂径定理可知M为AD的中点,由三角形的面积可求出CM的长,在Rt△ACM中,根据勾股定理可求出AM的长,进而可得出结论.
详解:∵在Rt△ABC中,∠ACB=90°,AC=3,BC=4,
∴AB=![]() =5,
=5,
过C作CM⊥AB,交AB于点M,如图所示,
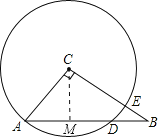
∵CM⊥AB,
∴M为AD的中点,
∵S△ABC=![]() ACBC=
ACBC=![]() ABCM,且AC=3,BC=4,AB=5,
ABCM,且AC=3,BC=4,AB=5,
∴CM=![]() ,
,
在Rt△ACM中,根据勾股定理得:AC2=AM2+CM2,即9=AM2+(![]() )2,
)2,
解得:AM=![]() ,
,
∴AD=2AM=![]() .
.
故选D.

练习册系列答案
相关题目
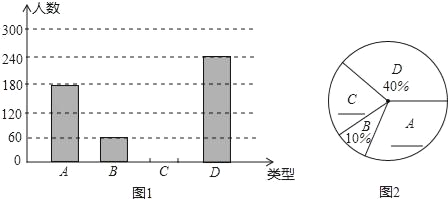
【题目】某大学举行了百科知识竞赛,为了解此次竞赛成绩的情况,随机抽取部分参赛学生的成绩,整理并制作出如下不完整的统计表和统计图,请根据图表信息解答以下问题:

组别 | 成绩 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
(1)表中![]() ___________.
___________.
(2)补全频数分布直方图
(3)计算扇形统计图中“![]() ”对应的圆心角度数.
”对应的圆心角度数.
(4)该大学共有![]() 人参加竞赛,若成绩在
人参加竞赛,若成绩在![]() 分以上(包括
分以上(包括![]() 分)的为“优”等,根据抽样结果,估计该校参赛学生成绩达到“优”等的人数.
分)的为“优”等,根据抽样结果,估计该校参赛学生成绩达到“优”等的人数.