题目内容
【题目】已知：抛物线 
与 
轴分别交于点A（-3，0），B（m，0）．将y1向右平移4个单位得到y2 ．
（1）求b的值；
（2）求抛物线y2的表达式；
（3）抛物线y2与 
轴交于点D，与 轴交于点E、F（点E在点F的左侧），记抛物线在D、F之间的部分为图象G（包含D、F两点），若直线 
与图象G有一个公共点，请结合函数图象，求直线 与抛物线y2的对称轴交点的纵坐标t的值或取值范围．
【答案】
（1）解：把A（-3，0）代入y1=x2+bx+3得：9-3b+3=0，
解得：b=4，
∴y1的表达式为：y=x2+4x+3
（2）解：将y1变形得：y1=（x+2）2-1
据题意y2=（x+2-4）2-1=（x-2）2-1=x2-4x+3；
∴抛物线y2的表达式为y=x2-4x+3
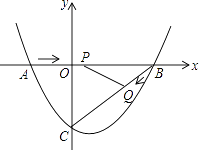
（3）解：∵y2=（x-2）2-1，函数图像如图所示：
∴对称轴是x=2，顶点为（2，-1）；
当y2=0时，x=1或x=3，
∴E（1，0），F（3，0），D（0，3），
∵直线y=kx+k-1过定点（-1，-1），
当直线y=kx+k-1与图象G有一个公共点时，t=-1，
当直线y=kx+k-1过F（3，0）时，3k+k-1=0，
解得：k= 
，
∴直线解析式为y= x- 
，
把x=2代入= x- ，得：y=- ，
当直线过D（0，3）时，k-1=3，
解得：k=4，
∴直线解析式为y=4x+3，
把x=2代入y=4x+3得：y=11，即t=11，
∴结合图象可知t=-1，或 ＜t≤11．
【解析】（1）把点A的坐标代入可求出b的值，即可得到函数解析式；
（2）先把y1的解析式化成顶点式，再根据平移规律可求出；
（3）画出函数y2的图象，可求出此函数与x轴、y轴的交点坐标；直线y=kx+k-1过定点（-1，-1），再根据直线y=kx+k-1与图象G有一个公共点可求出t=-1；再由直线y=kx+k-1过F（3，0）和过D（0，3），分别求出此直线的解析式，从而得出t的值，再结合图像进而可得出答案.
【考点精析】掌握二次函数图象的平移和抛物线与坐标轴的交点是解答本题的根本，需要知道平移步骤：（1）配方 y=a(x-h)2+k，确定顶点（h,k）（2）对x轴左加右减；对y轴上加下减；一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标．因此一元二次方程中的b2-4ac，在二次函数中表示图像与x轴是否有交点．当b2-4ac>0时，图像与x轴有两个交点；当b2-4ac=0时，图像与x轴有一个交点；当b2-4ac<0时，图像与x轴没有交点．
