Question

【题目】如图，在平面直角坐标系中，抛物线 与x轴交于点A（-2，0）、B（4，0）两点，与y轴交于点C．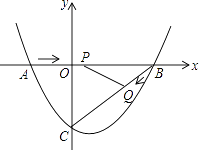

（1）求抛物线的表达式；
（2）点P从A点出发，在线段AB上以每秒3个单位长度的速度向B点运动，同时点Q从B点出发，在线段BC上以每秒1个单位长度向C点运动．其中一个点到达终点时，另一个点也停止运动．当△PBQ存在时，求运动多少秒使△PBQ的面积最大，最大面积是多少？
（3）当△PBQ的面积最大时，在BC下方的抛物线上存在点K，使 ，求K点坐标．

Answer 1

【答案】
（1）解：把点A（-2，0）、B（4，0）分别代入y=ax2+bx-3（a≠0），得

，

解得 ，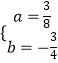

所以该抛物线的解析式为：y= x2- x-3

（2）解：设运动时间为t秒，则AP=3t，BQ=t．

∴PB=6-3t．

由题意得，点C的坐标为（0，-3）．

在Rt△BOC中，BC= =5．

如图1，过点Q作QH⊥AB于点H．

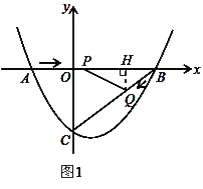
∴QH∥CO，

∴△BHQ∽△BOC，

∴ ，即 ，

∴HQ= t．

∴S△PBQ= PBHQ= （6-3t） t=- t2+ t=- （t-1）2+ ．

当△PBQ存在时，0＜t＜2

∴当t=1时，

S△PBQ最大= ．

答：运动1秒使△PBQ的面积最大，最大面积是

（3）解：设直线BC的解析式为y=kx+c（k≠0）．

把B（4，0），C（0，-3）代入，得

，

解得 ，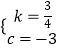

∴直线BC的解析式为y= x-3．

∵点K在抛物线上．

∴设点K的坐标为（m， m2- m-3）．

如图2，过点K作KE∥y轴，交BC于点E．

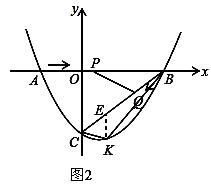
则点E的坐标为（m， m-3）．

∴EK= m-3-（ m2- m-3）=- m2+ m．

当△PBQ的面积最大时，∵S△CBK：S△PBQ=5：2，S△PBQ= ．

∴S△CBK= ．

S△CBK=S△CEK+S△BEK= EKm+ EK（4-m）

= ×4EK

=2（- m2+ m）

=- m2+3m．

即：- m2+3m= ．

解得 m1=1，m2=3．

∴K1（1，- ），K2（3，- ）．

【解析】（1）利用待定系数法可求出其解析式；
（2）过点Q作QH⊥AB于点H．由勾股定理可求出BC的长；设运动时间为t秒，可表示出AP、BQ、BP的长，再由△BHQ∽△BOC可表示出HQ的长，进而可得出△PBQ的面积S与t的关系式，由二次函数的最值可求出；
（3）先利用待定系数法求出直线BC的解析式.过点K作KE∥y轴，交BC于点E．根据点K在抛物线上，可设出K的坐标，则表示出E的坐标，进而表示出EK的值；根据△PBQ的面积最大时和已知可求出△CBK的面积，还可以用含有m的代数式表示出△CBK的面积，得到关于m的方程，解此方程求出m的值，从而求出k的坐标.
【考点精析】关于本题考查的确定一次函数的表达式和二次函数的最值，需要了解确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法；如果自变量的取值范围是全体实数，那么函数在顶点处取得最大值（或最小值），即当x=-b/2a时，y最值=(4ac-b2)/4a才能得出正确答案．