题目内容
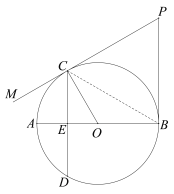
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,在⊙O的切线CM上取一点P,使得∠CPB=∠COA.
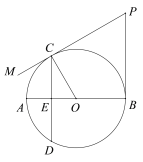
(1)求证:PB是⊙O的切线;
(2)若CD=6,∠AOC=60°,求PB的长.
【答案】(1)详见解析;(2)6
【解析】
(1)根据切线的性质和四边形的内角和即可得出∠PBO=90°,进而证得结论;
(2)解法1:连接OP,先根据垂径定理和30°的直角三角形的性质求出半径OC的长,即为OB的长,再利用四边形的内角和和切线长定理求出∠BPO的度数,进一步即可求出PB的长;
解法2:连接BC,先证明△PBC是等边三角形,再在直角△BCE中求出BC的长即可.
(1)证明: ∵ PC与⊙O相切于点C,∴ OC⊥PC,∴ ∠OCP=90°.
∵ ∠AOC=∠CPB,∠AOC+∠BOC=180°,
∴ ∠BOC+∠CPB=180°.
在四边形PBOC中,∠PBO=360°-∠CPB-∠BOC-∠PCO=90°.
∴ 半径OB⊥PB,∴ PB是⊙O的切线;
(2)解法1:连接OP,如图.
∵∠AOC=60°,∴∠BOC=120°.
∵ ∠OCP=∠OBP=90°,∴∠BPC=360°-120°-2×90°=60°.
∵ PB,PC都是⊙O的切线,∴ PO平分∠BPC,∴∠CPO=∠BPO=30°.
∵CD⊥AB,AB是⊙O的直径,CD=6,∴![]() ,
,
∵∠AOC=60°,CD⊥AB,∴∠ACO=30°,![]() =OB.
=OB.
∴PB= OB·![]() =
=![]() ·
·![]() = 6.
= 6.
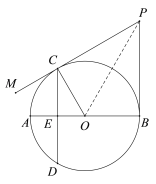
解法2:连接BC,如图.
∵∠AOC=60°,∴∠BOC=120°,
∵ ∠OCP=∠OBP=90°,∴∠BPC=360°-120°-2×90°=60°,
∵ PB,PC都是⊙O的切线,∴ PB=PC,
∴ △PBC为等边三角形,∴PB=BC.
∵CD⊥AB,AB是⊙O的直径,CD=6,∴![]() ,
,
∵∠AOC=60°,CD⊥AB,∴∠ABC=30°,
∴BC=2CE=6,∴PB= BC= 6.

 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案【题目】如图,等边△ABC的边长为3cm,点N在AC边上,AN=1cm.△ABC边上的动点M从点A出发,沿A→B→C运动,到达点C时停止.设点M运动的路程为xcm,MN的长为ycm.
小西根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小西的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了y与x的几组对应值;
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | 5.5 | 6 |
y/cm | 1 | 0.87 | 1 | 1.32 | 2.18 | 2.65 | 2.29 | 1.8 | 1.73 | 1.8 | 2 |
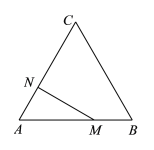
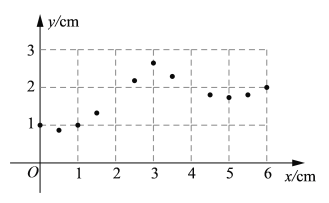
(2)在平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点,画出该函数的图象;
中,描出补全后的表中各组数值所对应的点,画出该函数的图象;
(3) 结合函数图象,解决问题:当MN=2cm时,点M运动的路程为 cm.