题目内容
【题目】对于平面直角坐标系xOy中的点P和⊙C,给出如下定义:若存在过点P的直线l交⊙C于异于点P的A,B两点,在P,A,B三点中,位于中间的点恰为以另外两点为端点的线段的中点时,则称点P为⊙C 的相邻点,直线l为⊙C关于点P的相邻线.
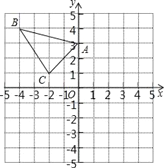
(1)当⊙O的半径为1时,
①分别判断在点D(![]() ,
, ![]() ),E(0,﹣
),E(0,﹣![]() ),F(4,0)中,是⊙O的相邻点有 ;
),F(4,0)中,是⊙O的相邻点有 ;
②请从①中的答案中,任选一个相邻点,在图1中做出⊙O关于它的一条相邻线,并说明你的作图过程;
③点P与点O的距离d满足范围___________________时,点P是⊙O的相邻点;
④点P在直线y=﹣x+3上,若点P为⊙O的相邻点,求点P横坐标x的取值范围;
(2)⊙C的圆心在x轴上,半径为1,直线y=﹣![]() x+2
x+2![]() 与x轴,y轴分别交于点M,N,若线段MN上存在⊙C的相邻点P,直接写出圆心C的横坐标x的取值范围.
与x轴,y轴分别交于点M,N,若线段MN上存在⊙C的相邻点P,直接写出圆心C的横坐标x的取值范围.

【答案】(1)①D、E ② 证明见解析;③ 0≤d≤3且d≠1 ④0≤x≤3;(2) 0≤x≤9
【解析】试题分析:(1)由相邻点的定义可知:在圆C内的点必为相邻点,在圆C外的点必须满足,2AB2=PC2-1,其中A为PB的中点,且AB≤2,所以若半径为1的圆C有相邻点P,则PC的长必须满足0≤PC≤3且PC≠1,分别求出D、E、F到⊙O的距离即可判断.求出直线y=-x+3与坐标轴的交点坐标分别为(0,3)和(3,0),根据(1)问中结论可知,P的横坐标的取值范围是:0≤x≤3;
(2)根据(1)问中可知:0≤PC≤3且PC≠1,又因为点P在线段MN上移动,所以点C在以点P为圆心,半径为3的圆内,且不能在以点P为圆心,半径为1的圆上,再根据点C在x轴上,即可得出C的横坐标取值范围.
试题解析:(1)由定义可知,
当点P在⊙C内时,
由垂径定理可知,点P必为⊙C的相邻点,
此时,0≤PC<1;
当点P在⊙C外时,设点A是PB的中点,连接PC交⊙C于点M,延长PC交⊙C于点N,连接AM,BN,

∵∠AMP+∠NMA=180°,
∠B+∠NMA=180°,
∴∠AMP=∠B,
∵∠P=∠P,
∴△AMP∽△NBP,
∴![]() ,
,
∴PAPB=PMPN,
∵点A是PB的中点,
∴AB=PA,
又∵⊙C的半径为1,
∴2AB2=(PC-CM)(PC+CN),
∴2AB2=PC2-1,
又∵AB是⊙C的弦,
∴AB≤2,
∴2AB2≤8,
∴PC2-1≤8,
∴PC2≤9,
∴PC≤3,
∵点P在⊙C外,
∴PC>1,
∴1<PC≤3,
当点P在⊙C上时,
此时PC=1,但不符合题意,
综上所述,半径为1的⊙C,当点P与圆心C的距离满足:0≤PC≤3,且PC≠1时,点P为⊙C的相邻点;

①∵D(![]() ,
, ![]() ),
),
∴DO= ,
,
∵E(0,-![]() ),
),
∴OE=![]() ,
,
∵F(4,0),
∴OF=4,
∴D和E是⊙O的相邻点;
②连接OD,过点D作OD的垂线交⊙O于A、B两点;

③令x=0代入y=-x+3,
∴y=3,
令y=0代入y=-x+3,
∴x=3,
∴y=-x+3与坐标轴的交点为(0,3)和(3,0)
∵由于点P在直线y=-x+3上,且点P是⊙O的相邻点,
∴0≤PO≤3,且PO≠1
又∵点P在⊙O外,
∴1<PO≤3,
∴p的横坐标范围为:0≤x≤3;
(2)令x=0代入y=-![]() x+2
x+2![]() ,
,
∴y=2![]() ,
,
∴N(0,2![]() ),
),
令y=0代入y=-![]() x+2
x+2![]() ,
,
∴x=6,
∴M(6,0),
∵点P是半径为1的⊙C的相邻点,
∴0≤PC≤3且PC≠1,
∴点C在以点P为圆心,半径为3的圆内,且不能在以点P为圆心,半径为1的圆上,
∵点C在x轴上,
∴点C的横坐标范围的取值范围:0≤x≤9.


 精英口算卡系列答案
精英口算卡系列答案