题目内容
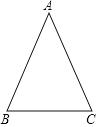
【题目】如图,△ABC是等腰三角形,AB=AC,∠A=36°.
(1)用尺规作∠ABC的角平分线BD,交AC于点D;(保留作图痕迹,不写作法);
(2)过点C作CE//BD,且CE=BD,求证:四边形BCED是菱形.
【答案】(1)答案见解析;(2)答案见解析
【解析】
(1)利用基本作图作∠ABC的平分线BD;
(2)先利用等腰三角形的性质和三角形内角和计算出∠ABC=∠BCA=![]() (180°﹣∠A)=72°,再利用角平分线定义得到∠CBD=∠ABD=36°,接着根据三角形外角性质得到∠BDC=72°,然后根据等腰三角形的判定定理得到BD=BC,再由四边形DBCE是平行四边形,即可得出结论.
(180°﹣∠A)=72°,再利用角平分线定义得到∠CBD=∠ABD=36°,接着根据三角形外角性质得到∠BDC=72°,然后根据等腰三角形的判定定理得到BD=BC,再由四边形DBCE是平行四边形,即可得出结论.
(1)如图,BD为所作;
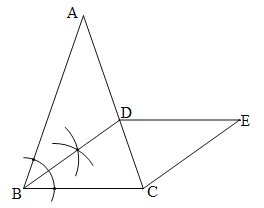
(2)∵AB=AC,∴∠ABC=∠BCA =![]() (180°﹣∠A)=
(180°﹣∠A)=![]() (180°﹣36°)=72°.
(180°﹣36°)=72°.
∵BD平分∠ABC,∴∠CBD=∠ABD=![]() ∠ABC=36°,∴∠BDC=∠A+∠ABD=36°+36°=72°,∴∠BCA =∠BDC,∴BD=BC.
∠ABC=36°,∴∠BDC=∠A+∠ABD=36°+36°=72°,∴∠BCA =∠BDC,∴BD=BC.
∵CE∥BD,CE=BD,∴四边形DBCE是平行四边形,∴平行四边形DBCE是菱形.

练习册系列答案
相关题目