题目内容
【题目】已知：∠MON＝45°，点A在OM上，点B、C在ON上，且OB＞OA，
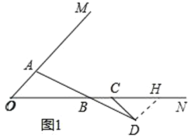
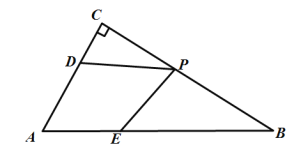
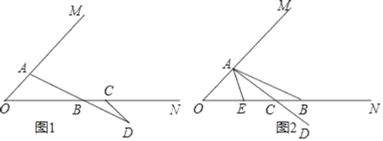
（1）如图1，当点C在点B的右侧时，在ON下方作∠NCD＝45°，交AB的延长线于点D．
①若AB＝BD，请直接写出线段OA和CD的关系 ；
②若AB＝
BD，判断线段OA和CD的关系，并说明理由；
③若AB＝10，BD＝8，OB＝14，则CD＝ ；
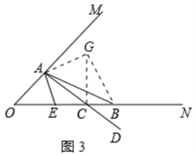
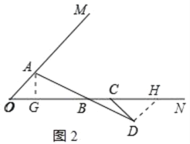
（2）如图2，当点C在点B的左侧时，在ON下方作∠NCD＝45°，CD的反向延长线交AB于点A，在∠OAB的内部作∠BAE＝45°，交ON于点E，则线段OE、EB、CB之间的数量关系是 ．
【答案】（1）①OA＝CD，OA⊥CD；②OA＝
CD，OA⊥CD，见解析；③
；（2） EB2＝OE2+CB2
【解析】
（1）①作DH∥OA交ON于H，通过证明△AOB≌△DHB（AAS），可得OA＝HD，再通过等边对等角和三角形内角和定理可得CD＝HD，∠CDH＝90°，即可得OA＝CD，CD⊥DH，再根据OA∥DH，即可得证OA⊥CD；②作DH∥OA交ON于H，通过证明△AOB∽△HDB，可得OA＝HD，再根据等边对等角和三角形内角和定理可得CD＝HD，∠CDH＝90°，即可得OA＝CD，CD⊥DH，再根据OA∥DH，即可得证OA⊥CD；③作DH∥OA交ON于H，作AG⊥OB于G，再根据等腰直角三角形的性质、勾股定理、相似三角形的性质求解即可；
（2）根据旋转的性质证明△BAE≌△BAG（SAS），从而可得EB＝GB，在Rt△GBC中，由勾股定理得：GB2＝CG2+CB2，即可得证EB2＝OE2+CB2．
解：（1）①结论：OA＝CD，OA⊥CD．理由如下：
作DH∥OA交ON于H．如图1所示：
∵DH∥OA，
∴∠MON＝∠BHD＝45°，
在△AOB和△DHB中，
，
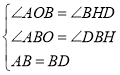∴△AOB≌△DHB（AAS），
∴OA＝HD，
∵∠NCD＝45°，
∴∠NCD＝∠BHD＝45°，
∴CD＝HD，∠CDH＝90°，
∴OA＝CD，CD⊥DH，
∵OA∥DH，
∴OA⊥CD；
故答案为：OA＝CD，OA⊥CD．
②结论：OA＝CD，OA⊥CD．
作DH∥OA交ON于H，如图1所示：
则△AOB∽△HDB，
∴
，
∴OA＝HD，
∵∠NCD＝∠AOB＝∠BHD＝45°，
∴CD＝HD，∠CDH＝90°，
∴OA＝CD，CD⊥DH
∵OA∥DH，
∴OA⊥CD；
③作DH∥OA交ON于H，作AG⊥OB于G，如图2所示：
则△AOG是等腰直角三角形，
∴AG＝OG，在Rt△ABG中，
由勾股定理得：AG2+BG2＝AB2，即AG2+（14﹣AG）2＝102，
解得：AG＝6，或AG＝8（舍去），
∴AG＝6，
∴OA＝
AG＝6，
∵DH∥OA，
∴△AOB∽△HDB，
∴
，即
，
解得：HD＝，
∵∠NCD＝∠AOB＝∠BHD＝45°，
∴CD＝HD＝；
故答案为：；
（2）结论：EB2＝OE2+CB2．理由如下：
∵∠AOB＝∠NCD＝∠ACO′＝45°，
∴△AOC是等腰直角三角形，
将△AOE绕点A逆时针旋转90°得到△ACG，连接BG，如图3所示：
则∠ACG＝∠AOB＝45°，AG＝AE，CG＝OE，
∵∠ACO＝∠BCD＝45°，
∴∠GCO＝45°+45°＝90°，
∴∠GCB＝90°，
∵∠BAE＝45°，∠EAG＝90°，
∴∠BAG＝45°＝∠BAE，
在△BAE和△BAG中，
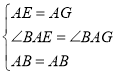
∴△BAE≌△BAG（SAS），
∴EB＝GB，
在Rt△GBC中，由勾股定理得：GB2＝CG2+CB2，
∴EB2＝OE2+CB2．
故答案为：EB2＝OE2+CB2．
