题目内容
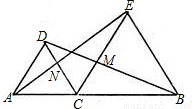
如图,△ACD、△BCE都是等边三角形,△NCE经过旋转后能与△MCB重合.请回答:(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)若NE=10cm,则MB等于多少?
【答案】分析:(1)已知旋转的两个三角形,观察图形,得出旋转中心;
(2)M、N是对应点,∠MCN为旋转角,利用平角可计算旋转角的度数;
(3)根据旋转图形全等,可知MB=NE.
解答:解:观察图形可知:
(1)旋转中心是点C;
(2)∵∠MCN=180°-∠ACN-∠BCM=180°-60°-60°=60°,
∴旋转了60度;
(3)∵△NCE经过旋转后能与△MCB重合,
∴△NCE≌△MCB,
∴MB=NE=10cm.
点评:旋转的性质:旋转前后图形全等,对应点与旋转中心的连线相等,夹角为旋转角.
(2)M、N是对应点,∠MCN为旋转角,利用平角可计算旋转角的度数;
(3)根据旋转图形全等,可知MB=NE.
解答:解:观察图形可知:
(1)旋转中心是点C;
(2)∵∠MCN=180°-∠ACN-∠BCM=180°-60°-60°=60°,
∴旋转了60度;
(3)∵△NCE经过旋转后能与△MCB重合,
∴△NCE≌△MCB,
∴MB=NE=10cm.
点评:旋转的性质:旋转前后图形全等,对应点与旋转中心的连线相等,夹角为旋转角.

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
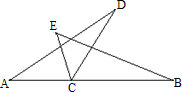 5、如图,△ACD≌△ECB,A,C,B在一条直线上,且A和E是一对对应顶点,如果∠BCE=130°,那么将△ACD围绕C点顺时针旋转( )与△ECB重合.
5、如图,△ACD≌△ECB,A,C,B在一条直线上,且A和E是一对对应顶点,如果∠BCE=130°,那么将△ACD围绕C点顺时针旋转( )与△ECB重合. 21、如图,∠ACD是△ABC的一个外角,请你从下面三个条件中,选出两个作为已知条件,另一个作为结论,推出一个正确的命题.
21、如图,∠ACD是△ABC的一个外角,请你从下面三个条件中,选出两个作为已知条件,另一个作为结论,推出一个正确的命题.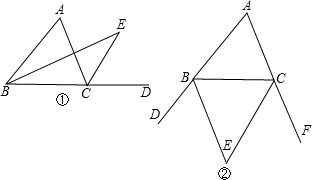
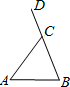 (2011•安宁市一模)如图,∠ACD是等腰△ABC的一个外角,已知AB=AC,∠A=50°,那么∠ACD=( )
(2011•安宁市一模)如图,∠ACD是等腰△ABC的一个外角,已知AB=AC,∠A=50°,那么∠ACD=( ) 如图,∠ACD是△ABC的外角,∠A=50°,∠ACD=110°,
如图,∠ACD是△ABC的外角,∠A=50°,∠ACD=110°,