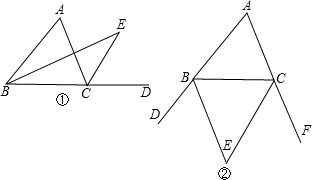
题目内容
如图①,∠ACD是△ABC的外角,BE平分∠ABC,CE平分∠ACD,且BE、CE交于点E.(1)如果∠A=60°,∠ABC=50°,求∠E的度数;
(2)猜想:∠E与∠A有什么数量关系;(写出结论即可)
(3)如图②,点E是△ABC两外角平分线BE、CE的交点,探索∠E与∠A之间的数量关系,并说明理由.
分析:此类题运用三角形的内角和定理及其推论,和角平分线的定义即可解决.
解答: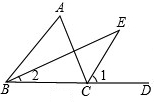 解:(1)根据外角的性质得∠ACD=∠A+∠ABC=60°+50°=110°,
解:(1)根据外角的性质得∠ACD=∠A+∠ABC=60°+50°=110°,
∵BE平分∠ABC,CE平分∠ACD,
∴∠1=
∠ACD=55°,∠2=
∠ABC=25°
∵∠E+∠2=∠1,
∴∠E=∠1-∠2=30°;
(2)猜想:∠E=
∠A;
(3)∵BE、CE是两外角的平分线,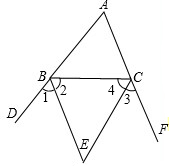
∴∠2=
∠CBD,∠4=
∠BCF,
而∠CBD=∠A+∠ACB,∠BCF=∠A+∠ABC,
∴∠2=
(∠A+∠ACB),∠4=
(∠A+∠ABC).
∵∠E+∠2+∠4=180°,
∴∠E+
(∠A+∠ACB)+
(∠A+∠ABC)=180°,
即∠E+
∠A+
(∠A+∠ACB+∠ABC)=180°.
∵∠A+∠ACB+∠ABC=180°,
∴∠E+
∠A=90°.
 解:(1)根据外角的性质得∠ACD=∠A+∠ABC=60°+50°=110°,
解:(1)根据外角的性质得∠ACD=∠A+∠ABC=60°+50°=110°,∵BE平分∠ABC,CE平分∠ACD,
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠E+∠2=∠1,
∴∠E=∠1-∠2=30°;
(2)猜想:∠E=
| 1 |
| 2 |
(3)∵BE、CE是两外角的平分线,

∴∠2=
| 1 |
| 2 |
| 1 |
| 2 |
而∠CBD=∠A+∠ACB,∠BCF=∠A+∠ABC,
∴∠2=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠E+∠2+∠4=180°,
∴∠E+
| 1 |
| 2 |
| 1 |
| 2 |
即∠E+
| 1 |
| 2 |
| 1 |
| 2 |
∵∠A+∠ACB+∠ABC=180°,
∴∠E+
| 1 |
| 2 |
点评:特别注意此题中发现的结论,充分运用三角形的内角和定理及其推论结合三角形的角平分线概念导出:图①中,∠E=
∠A;图②中,∠E=90°-
∠A.
| 1 |
| 2 |
| 1 |
| 2 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2010•雅安)如图,点C是线段AB上除点A、B外的任意一点,分别以AC、BC为边在线段AB的同旁作等边△ACD和等边△BCE,连接AE交DC于M,连接BD交CE于N,连接MN.
(2010•雅安)如图,点C是线段AB上除点A、B外的任意一点,分别以AC、BC为边在线段AB的同旁作等边△ACD和等边△BCE,连接AE交DC于M,连接BD交CE于N,连接MN. 如图,△ABE≌△ACD,点B、C是对应顶点,∠A=40°,∠B=30°,则∠ADC=
如图,△ABE≌△ACD,点B、C是对应顶点,∠A=40°,∠B=30°,则∠ADC=
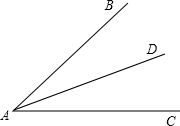 如图,射线AD是∠BAC的角平分线,已知∠ACD度数是α,那么要使AB∥CD,∠ADC的度数必须是
如图,射线AD是∠BAC的角平分线,已知∠ACD度数是α,那么要使AB∥CD,∠ADC的度数必须是 的平分线交于点An. 设∠A=
的平分线交于点An. 设∠A=