Question

【题目】如图，在矩形ABCD中，AB=5，AD=3，点P是AB边上一点（不与A，B重合），连接CP，过点P作PQ⊥CP交AD边于点Q，连接CQ．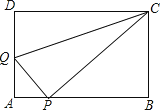

（1）当△CDQ≌△CPQ时，求AQ的长；
（2）取CQ的中点M，连接MD，MP，若MD⊥MP，求AQ的长．

Answer 1

【答案】
（1）

【解答】解：∵△CDQ≌△CPQ，

∴DQ=PQ，PC=DC，

∵AB=DC=5，AD=BC=3，

∴PC=5，

在Rt△PBC中，PB==4，

∴PA=AB﹣PB=5﹣4=1，

设AQ=x，则DQ=PQ=3﹣x，

在Rt△PAQ中，（3﹣x）2=x2+12，

解得x=，

∴AQ=．

（2）

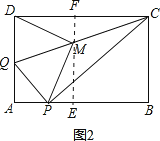
如图2，过M作EF⊥CD于F，则EF⊥AB，

∵MD⊥MP，

∴∠PMD=90°，

∴∠PME+∠DMF=90°，

∵∠FDM+∠DMF=90°，

∴∠MDF=∠PME，

∵M是QC的中点，

根据直角三角形直线的性质求得DM=PM=QC，

在△MDF和△PME中，

，

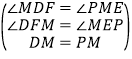∴△MDF≌△PME（AAS），

∴ME=DF，PE=MF，

∵EF⊥CD，AD⊥CD，

∴EF∥AD，

∵QM=MC，

∴DF=CF=DC=，

∴ME=，

∵ME是梯形ABCQ的中位线，

∴2ME=AQ+BC，即5=AQ+3，

∴AQ=2．

【解析】（1）根据全等三角形的性质求得DQ=PQ，PC=DC=5，然后利用勾股定理即可求得；
（2）过M作EF⊥CD于F，则EF⊥AB，先证得△MDF≌△PME，求得ME=DF=，然后根据梯形的中位线的性质定理即可求得．
【考点精析】通过灵活运用勾股定理的概念和矩形的性质，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；矩形的四个角都是直角，矩形的对角线相等即可以解答此题．