题目内容
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=6cm,点D、E在边AC上,AD=4cm,点E是CD的中点,以DE为边的矩形DEFG的顶点G在边AB上,动点P从点A出发,以1cm/s的速度沿AC向点C运动,过点P作PQ∥AB交BC于点Q,设点P的运动时间为t(s),矩形DEFG与△PCQ重叠部分图形的面积为s(cm2).
(1)在点P的运动过程中,当线段PQ与矩形DEFG的边DG有交点,令交点为H,用含t的代数式表示线段DH的长.
(2)求s与t的函数关系式.
(3)点P出发的同时,动点M从点D出发,以acm/s的速度沿D-G-F-E-F运动,点N是线段PQ中点,在点P的运动过程中,若点M、N能够重合在矩形DEFG的边上,求动点M的速度a.
【答案】(1)3-![]() t,(2)当0<t≤2时,S= 6-
t,(2)当0<t≤2时,S= 6-![]() t2,当2<t≤4时,S=
t2,当2<t≤4时,S= ![]() -
-![]() t,当4<t≤6时,S=
t,当4<t≤6时,S=![]() t2-
t2-![]() t+
t+![]() ,当6<t≤8时,S=0,(3)a=
,当6<t≤8时,S=0,(3)a=![]() 或a=
或a=![]() .
.
【解析】
试题分析:(1)由△ADG∽△ACB求出DG,再由△PDH∽ADG,求出DH,即可;
(2)分四段当0<t≤2时,当2<t≤4时,当4<t≤6时,当6<t≤8时分别求出面积即可;
(3)先判断出,只有点M在EF上时,点P与D重合,M,N才能重合,此时t=4,点M走的路程为at.依题意,由at=8-![]() 或at=8+
或at=8+![]() .
.
试题解析:(1)由运动有,AP=t,AD=4,
∴PD=4-t,
∵△ADG∽△ACB,
∴![]() ,
,
∴DG=3,
∵△PDH∽ADG,
∴![]() ,
,
∴![]() ,
,
∴DH=![]() (4-t)=3-
(4-t)=3-![]() t,
t,
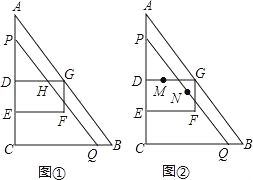
(2)当0<t≤2时,如图1,

S=S四边形DEFG-S△GFH=3×2-![]() t×
t×![]() t=6-
t=6-![]() t2,
t2,
当2<t≤4时,如图2,

S=S四边形DEFG=![]() ×2[
×2[![]() (4-t)+
(4-t)+![]() (6-t)]=
(6-t)]=![]() -
-![]() t,
t,
当4<t≤6时,如图3,
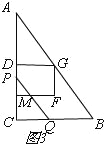
S=S△GFH=![]() ×(6-t)×
×(6-t)×![]() (6-t)=
(6-t)=![]() t2-
t2-![]() t+
t+![]() ,
,
当6<t≤8时,S=0,
(3)由题意知,只有点M在EF上时,点P与D重合,M,N才能重合,此时t=4,
点M走的路程为at.依题意,由at=8-![]() 或at=8+
或at=8+![]() ,
,
∴a=![]() 或a=
或a=![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案