Question

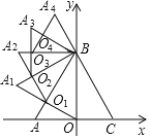
【题目】如图，在平面直角坐标系中，正方形的顶点A的坐标为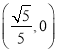，顶点D的坐标为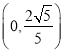，延长交轴于点A，作正方形，延长交轴于点，作正方形，按这样的规律进行下去，第2021个正方形的周长为（ ）

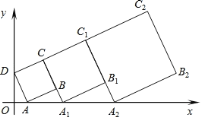
A.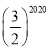B.C.D.

Answer 1

【答案】C

【解析】

推出AD＝AB，∠DAB＝∠ABC＝∠ABA1＝90°＝∠DOA，求出∠ADO＝∠BAA1，证△DOA∽△ABA1，得出＝＝，求出AB，BA1，求出边长A1C＝，求出周长即可；求出第2个正方形的边长是（）2，求出周长，再求出第3个正方形的周长；依此类推得出第2021个正方形的边长，求出周长即可．

解：∵四边形ABCD是正方形，

∴AD＝AB，∠DAB＝∠ABC＝∠ABA1＝90°＝∠DOA，

∴∠ADO+∠DAO＝90°，∠DAO+∠BAA1＝90°，

∴∠ADO＝∠BAA1，

∵∠DOA＝∠ABA1，

∴△DOA∽△ABA1，

∴＝＝，

∵AB＝AD＝＝1，

∴BA1＝，

∴第2个正方形A1B1C1C的边长A1C＝A1B+BC＝+1＝，周长是4×，

同理第3个正方形的边长是，周长是4×（）2；

第4个正方形的边长是（）3，周长是4×（）3；

…，

第2021个正方形的边长是（）2020，周长是4×（）2020，

故选：C．