Question

【题目】问题提出

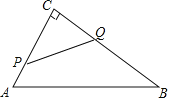
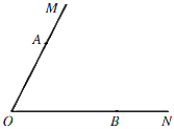
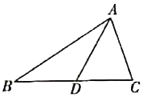
（1）如图，是的中线，则__________；（填“”“”或“”）

问题探究

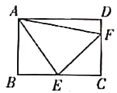
（2）如图，在矩形中，，点为的中点，点为上任意一点，当的周长最小时，求的长；

问题解决

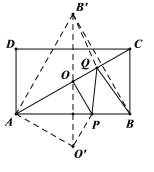
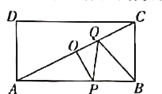
（3）如图，在矩形中，，点为对角线的中点，点为上任意一点，点为上任意一点，连接，是否存在这样的点，使折线的长度最小？若存在，请确定点的位置，并求出折线的最小长度；若不存在，请说明理由．

Answer 1

【答案】（1）＞；（2）；（3）当点与的中点重合时，折线的长度最小，最小长度为4．

【解析】

（1）如图（见解析），先根据三角形全等的判定定理与性质得出，再根据三角形的三边关系定理即可得；

（2）如图（见解析），先根据矩形的性质得出，从而可得AE的长，再根据三角形的周长公式、两点之间线段最短得出的周长最小时，点F的位置，然后利用相似三角形的判定与性质即可得；

（3）如图（见解析），先根据轴对称性质、两点之间线段最短得出折线的长度最小时，四点共线，再利用直角三角形的性质、矩形的性质得出，，，然后利用轴对称的性质、角的和差可得，，由此利用勾股定理可求出的长，即折线的最小长度；设交于点，根据等边三角形的判定与性质可得，从而可得，由此即可得折线的长度最小时，点Q的位置．

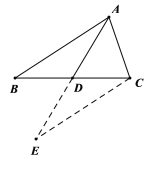
（1）如图，延长AD，使得，连接CE

是的中线

在和中，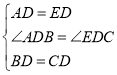

在中，由三角形的三边关系定理得：，即

故答案为：；

（2）如图，作点关于的对称点，连接FG，则

四边形ABCD是矩形，

垂直平分

点E是BC的中点

，，

则的周长为

要使的周长最小，只需

由两点之间线段最短可知，当点共线时，取得最小值

∴

∴，即

解得；

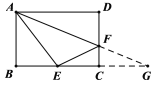
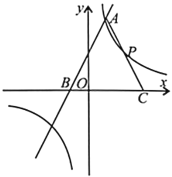
（3）如图，作点关于的对称点，作点关于的对称点，连接，则

∴折线的长度为

由两点之间线段最短可知，，当且仅当点四点共线时，折线取得最小长度为

∵在矩形中，

∴，

∵点为的中点

∴

∵点与点关于对称，点与点关于对称

∴，

，

∴

设交于点

在中，

∴

，即

又∵

∴是等边三角形

∴

∵

∴点与的中点重合

综上，当点与的中点重合时，折线的长度最小，最小长度为4．