��Ŀ����
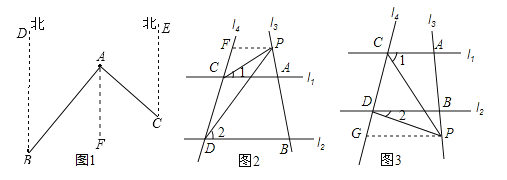
����Ŀ����ͼ�٣���ֱ֪��l1��l2����l3��l1��l2�ֱ��ཻ��A��B���㣬l4��l1��l2�ֱ���C��D���㣬��ACP����1����BDP����2����CPD����3��
��P���߶�AB����
(1)����1��22������2��33�������3��________��
(2)���ҳ���1����2����3֮��ĵ�����ϵ����˵�����ɣ�
(3)Ӧ��(2)�еĽ��۽������������
��ͼ������A��B����ƫ��40���ķ����ϣ���C���ı�ƫ��45���ķ����ϣ����BAC�Ķ�����
(4)�����P��ֱ��l3������A��B��������˶�ʱ�������������䣬��̽����1����2����3֮��Ĺ�ϵ(��P��A��B���㲻�غ�)��ֱ��д�����ۼ��ɣ�



���𰸡���1��55�㣻��2����1+��2=��3����3��85�㣻��4����CPD=|��1����2|.
�������������������1������ƽ���ߵ����ʺ��������ڽǺͶ������������
��2������ƽ���ߵ����ʺ��������ڽǺͶ������������
��3����A����AF��BD����AF��BD��CE������ƽ���ߵ����ʼ��������
��4���ֵ�P����A������뵱P����B���������������з������ۼ��ɣ�
���������������1����1+��2=��3��
��l1��l2�����1+��PCD+��PDC+��2=180��������PCD������3+��PCD+��PDC=180�������3=��1+��2=55�����ʴ�Ϊ��55����
��2����1+��2=��3������������
��l1��l2�����1+��PCD+��PDC+��2=180��������PCD������3+��PCD+��PDC=180�������1+��2=��3��
��3����A����AF��BD����AF��BD��CE������BAC=��DBA+��ACE=40��+45��=85����
��4����P����A�����ʱ����ͼ2����P��PF��l1����l4��F�����1=��FPC��
��l1��l4����PF��l2�����2=��FPD��
�ߡ�CPD=��FPD����FPC�����CPD=��2����1��
��P����B�����ʱ����ͼ3����P��PG��l2����l4��G�����2=��GPD��
��l1��l2����PG��l1�����1=��CPG��
�ߡ�CPD=��CPG����GPD�����CPD=��1����2��
������������CPD=|��1����2|��

 ��У����ϵ�д�
��У����ϵ�д�