题目内容
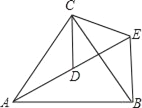
【题目】如图,在四边形ABCD中,∠D=90°,AC平分∠DAB,且点C在以AB为直径的⊙O上. 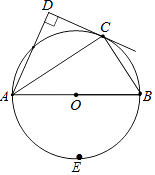
(1)求证:CD是⊙O的切线;
(2)点E是⊙O上一点,连接BE,CE.若∠BCE=42°,cos∠DAC= ![]() ,AC=m,写出求线段CE长的思路.
,AC=m,写出求线段CE长的思路.
【答案】
(1)解:证明:连接OC,如图1中.
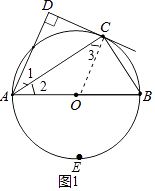
∵AC平分∠DAB,
∴∠1=∠2,
∵OA=OC,
∴∠3=∠2,
∴∠3=∠1,
∴AD∥OC,
∴∠OCD=∠D=90°,
又∵OC是⊙O的半径,
∴CD是⊙O的切线.
(2)解:求解思路如下:
过点B作BF⊥CE于F,如图.
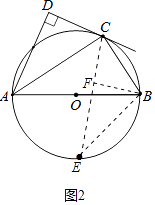
①在Rt△ACB中,根据BC=ACtan∠CAB,求出BC.
②在Rt△CFB中,由∠BCF=42°及BC的长,可求CF,BF的长;
③在Rt△EFB中,由∠E的三角函数值及BF的长,可EF的长;
④由CE=CF+EF,可求CE的长
【解析】(1)连接OC,如图1中.只要证明OC∥AD,由AD⊥CD,即可证明OC⊥CD解决问题.(2)过点B作BF⊥CE于F,如图2中.①在Rt△ACB中,根据BC=ACtan∠CAB,求出BC.②在Rt△CFB中,由∠BCF=42°及BC的长,可求CF,BF的长;③在Rt△EFB中,由∠E的三角函数值及BF的长,可EF的长;④由CE=CF+EF,可求CE的长.
【考点精析】解答此题的关键在于理解解直角三角形的相关知识,掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).

练习册系列答案
相关题目