Question

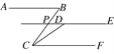
【题目】如图，已知AB∥CF，DE∥CF，DE与BC交于点P，若∠ABC＝70°，∠CDE＝130°.

(1)试判断∠ABP与∠BPD之间的数量关系，并说明理由；

(2)求∠BCD的度数．

Answer 1

【答案】(1)∠ABP＝∠BPD，理由见解析；(2)∠BCD＝20°.

【解析】

（1）根据AB∥CF，DE∥CF，可得AB∥DE，进而得出∠ABP=∠BPD；

（2）由AB∥CF，∠ABC=70°，易求∠BCF，又DE∥CF，∠CDE=130°，那么易求∠DCF，于是∠BCD=∠BCF-∠DCF可求．

（1）∠ABP＝∠BPD，

理由：∵AB∥CF，DE∥CF，

∴AB∥DE，

∴∠ABP＝∠BPD；

（2）∵AB∥CF，∠ABC＝70°，

∴∠BCF＝∠ABC＝70°，

又∵DE∥CF，∠CDE＝130°，

∴∠DCF＋∠CDE＝180°，

∴∠DCF＝50°，

∴∠BCD＝∠BCF－∠DCF＝70°－50°＝20°.