��Ŀ����
����Ŀ��ʹ�ú���ֵΪ����Ա�����ֵ��Ϊ��������㣮���磬���ں���y��x��1����y��0�ɵ�x��1�����Ǿ�˵1�Ǻ���y��x��1����㣮
��֪y��x2��2mx��2(m��3)(mΪ����)��
(1)��m��0ʱ����ú�������㣻
(2)֤��������mȡ��ֵ���ú�������������㣻
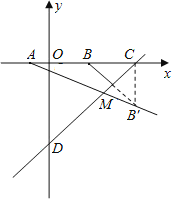
(3)�躯�����������ֱ�Ϊx1��x2����![]() ����ʱ����ͼ����x��Ľ���ֱ�ΪA��B(��A�ڵ�B���)����M��ֱ��y��x��10�ϣ���MA��MB��Сʱ����ֱ��AM�ĺ�������ʽ��
����ʱ����ͼ����x��Ľ���ֱ�ΪA��B(��A�ڵ�B���)����M��ֱ��y��x��10�ϣ���MA��MB��Сʱ����ֱ��AM�ĺ�������ʽ��
���𰸡���1��![]() ��-
��-![]() ��2��y=-
��2��y=-![]() x-1
x-1
�������������������1���������и����ĺ��������Ķ��壬��m=0����y=x2-2mx-2��m+3����Ȼ����y=0���ɽ�ú�������㣻
��2����y=0��������ΪһԪ���η��̣�Ҫ��֤�������������⣬ֻ��֤������0���ɣ�
��3�������������������������ʽ�������A��B�������꣬��������B����ֱ��y=x-10�ĶԳƵ�B��������AB���������B�������꼴����õ�MA+MB��Сʱ��ֱ��AM�ĺ�������ʽ��
�����������1����![]() =0ʱ���ú���Ϊ
=0ʱ���ú���Ϊ![]() ����
����![]() =0���ɵ�
=0���ɵ�![]() ��
��
����![]() =0ʱ����ú��������Ϊ
=0ʱ����ú��������Ϊ![]() ��
��![]() ��
��
��2����![]() =0������=
=0������=![]() ��
��
������![]() ȡ��ֵ������
ȡ��ֵ������![]() ������������ȵ�ʵ������
������������ȵ�ʵ������
������![]() ȡ��ֵ���ú��������������
ȡ��ֵ���ú��������������
��3����������![]() ��
��![]()
��![]() ��
��![]() ����
����![]() �����
�����![]() ��
��
�������Ľ���ʽΪ![]() ��
��![]() =0�����
=0�����![]() ��
��
����A�ڵ�B��࣬��A(![]() )��B(4��0)��
)��B(4��0)��
����B����ֱ��![]() �ĶԳƵ�B��������AB������AB����ֱ��
�ĶԳƵ�B��������AB������AB����ֱ��![]() �Ľ����������������M�㡣�����ֱ��
�Ľ����������������M�㡣�����ֱ��![]() ��
��![]() �ᡢ
�ᡢ![]() ��Ľ���ֱ�ΪC��10,0����D��0,10����Z.X.X.K]
��Ľ���ֱ�ΪC��10,0����D��0,10����Z.X.X.K]
����CB��������BCD=45������BC=CB��=6����B��CD=��BCD=45����
���BCB��=90������B����![]() ������ֱ��AB���Ľ���ʽΪ
������ֱ��AB���Ľ���ʽΪ![]() ����Z-X-X-K]
����Z-X-X-K]
![]() �����
�����![]() ��ֱ��AB���Ľ���ʽΪ
��ֱ��AB���Ľ���ʽΪ![]() ��
��
��AM�Ľ���ʽΪ![]()