��Ŀ����
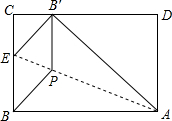
��ƽ��ֱ������ϵ�У�����OACB�Ķ���O������ԭ�㣬����A��B�ֱ���x�ᡢy����������ϣ�OA=3��OB=4��DΪ��OB���е㣮

��1����EΪ��OA�ϵ�һ�����㣬����CDE���ܳ���Сʱ�����E�����ꣻ
��2����E��FΪ��OA�ϵ��������㣬��EF=2�����ı���CDEF���ܳ���Сʱ�����E��F�����꣮
����ܰ��ʾ����������D����x��ĶԳƵ�D�䣬����CD����x�ύ�ڵ�E����ʱ��CDE���ܳ�����С�ģ���������ֻ�����OE�ij����Ϳ���ȷ����E�������ˣ���

��1����EΪ��OA�ϵ�һ�����㣬����CDE���ܳ���Сʱ�����E�����ꣻ
��2����E��FΪ��OA�ϵ��������㣬��EF=2�����ı���CDEF���ܳ���Сʱ�����E��F�����꣮
����ܰ��ʾ����������D����x��ĶԳƵ�D�䣬����CD����x�ύ�ڵ�E����ʱ��CDE���ܳ�����С�ģ���������ֻ�����OE�ij����Ϳ���ȷ����E�������ˣ���
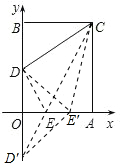
��1����ͼ������D����x��ĶԳƵ�D'������CD'��x�ύ�ڵ�E������DE��
���ڱ�OA����ȡ��E'���E���غϣ�����CE'��DE'��D'E'
��DE'+CE'=D'E'+CE'��CD'=D'E+CE=DE+CE��
��֪��CDE���ܳ���С��
���ھ���OACB�У�OA=3��OB=4��DΪOB���е㣬
��BC=3��D'O=DO=2��D'B=6��
��OE��BC��
��Rt��D'OE��Rt��D'BC����
=
��OE=
=
=1
���E��������1��0����
��2����ͼ������D����x��ĶԳƵ�D'����CB���Ͻ�ȡCG=2������D'G��x�ύ�ڵ�E����EA�Ͻ�ȡEF=2��
��GC��EF��GC=EF��
���ı���GEFCΪƽ���ı��Σ���GE=CF��
��DC��EF�ij�Ϊ��ֵ��
���ʱ�õ��ĵ�E��Fʹ�ı���CDEF���ܳ���С��
��OE��BC��
��Rt��D'OE��Rt��D'BG����
=
��
��OE=
=
=
=
��OF=OE+EF=
+2=
���E��������
��0������F��������
��0����10�֣�
���ڱ�OA����ȡ��E'���E���غϣ�����CE'��DE'��D'E'
��DE'+CE'=D'E'+CE'��CD'=D'E+CE=DE+CE��
��֪��CDE���ܳ���С��
���ھ���OACB�У�OA=3��OB=4��DΪOB���е㣬
��BC=3��D'O=DO=2��D'B=6��
��OE��BC��
��Rt��D'OE��Rt��D'BC����
| OE |
| BC |
| D��O |
| D��B |
��OE=
| D��O•BC |
| D��B |
| 2��3 |
| 6 |
���E��������1��0����
��2����ͼ������D����x��ĶԳƵ�D'����CB���Ͻ�ȡCG=2������D'G��x�ύ�ڵ�E����EA�Ͻ�ȡEF=2��

��GC��EF��GC=EF��
���ı���GEFCΪƽ���ı��Σ���GE=CF��
��DC��EF�ij�Ϊ��ֵ��
���ʱ�õ��ĵ�E��Fʹ�ı���CDEF���ܳ���С��
��OE��BC��
��Rt��D'OE��Rt��D'BG����
| OE |
| BG |
| D��O |
| D��B |
��OE=
| D��O•BG |
| D��B |
| D��O•(BC-CG) |
| D��B |
| 2��1 |
| 6 |
| 1 |
| 3 |
��OF=OE+EF=
| 1 |
| 3 |
| 7 |
| 3 |
���E��������
| 1 |
| 3 |
| 7 |
| 3 |


��ϰ��ϵ�д�
�����Ŀ