题目内容
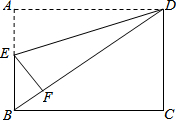
矩形纸片ABCD中,AB=5,AD=4,将纸片折叠,使点B落在边CD上的B′处,折痕为AE,点P是AE上的一点,且BP=BE,连接B′P.
(1)求B′D的长;
(2)求证:四边形BPB′E的形状为菱形;
(3)若在折痕AE上存在一点到边CD的距离与到点B的距离相等,请直接写出此相等距离的值.
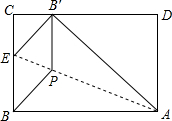
(1)求B′D的长;
(2)求证:四边形BPB′E的形状为菱形;
(3)若在折痕AE上存在一点到边CD的距离与到点B的距离相等,请直接写出此相等距离的值.

(1)∵四边形ABCD是矩形,
∴∠D=90°,
由折叠的性质可得:AB′=AB=5,
在Rt△ADB′中,B′D=
=3;
(2)证明:由折叠的性质可得:BP=B′P,BE=B′E,
∵BP=BE,
∴BP=B′P=B′E=BE,
∴四边形BPB′E的形状为菱形;
(3)存在.
∵四边形BPB′E的形状为菱形,
∴BE∥B′P,BP=B′P,
∴BC⊥CD,
∴B′P⊥CD,
∴点P到边CD的距离与到点B的距离相等,
设BP=x,
则B′E=x,
∵B′C=CD-B′D=5-3=2,CE=BC-BE=4-x,
在Rt△B′CE中,B′E2=CE2+B′C2,
∴x2=(4-x)2+22,
解得:x=2.5,
∴此相等距离的值为2.5.
∴∠D=90°,
由折叠的性质可得:AB′=AB=5,
在Rt△ADB′中,B′D=
| AB′2-AD2 |
(2)证明:由折叠的性质可得:BP=B′P,BE=B′E,
∵BP=BE,
∴BP=B′P=B′E=BE,
∴四边形BPB′E的形状为菱形;
(3)存在.
∵四边形BPB′E的形状为菱形,
∴BE∥B′P,BP=B′P,
∴BC⊥CD,
∴B′P⊥CD,
∴点P到边CD的距离与到点B的距离相等,
设BP=x,
则B′E=x,
∵B′C=CD-B′D=5-3=2,CE=BC-BE=4-x,
在Rt△B′CE中,B′E2=CE2+B′C2,
∴x2=(4-x)2+22,
解得:x=2.5,
∴此相等距离的值为2.5.

练习册系列答案
相关题目