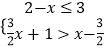题目内容
【题目】已知当x1=a,x2=b,x3=c时,二次函数y= ![]() x2+mx对应的函数值分别为y1 , y2 , y3 , 若正整数a,b,c恰好是一个三角形的三边长,且当a<b<c时,都有y1<y2<y3 , 则实数m的取值范围是 .
x2+mx对应的函数值分别为y1 , y2 , y3 , 若正整数a,b,c恰好是一个三角形的三边长,且当a<b<c时,都有y1<y2<y3 , 则实数m的取值范围是 .
【答案】m>﹣ ![]()
【解析】方法一: 解:∵正整数a,b,c恰好是一个三角形的三边长,且a<b<c,
∴a最小是2,
∵y1<y2<y3 ,
∴﹣ ![]() <2.5,
<2.5,
解得m>﹣2.5.
方法二:
解:当a<b<c时,都有y1<y2<y3 ,
即 ![]() ,
,
∴ 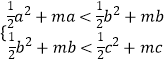 ,
,
∴ 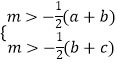 ,
,
∵a,b,c恰好是一个三角形的三边长,a<b<c,
∴a+b<b+c,
∴m>﹣ ![]() (a+b),
(a+b),
∵a,b,c为正整数,
∴a,b,c的最小值分别为2、3、4,
∴m>﹣ ![]() (a+b)≥﹣
(a+b)≥﹣ ![]() (2+3)=﹣
(2+3)=﹣ ![]() ,
,
∴m>﹣ ![]() ,
,
故答案为:m>﹣ ![]() .
.
根据三角形的任意两边之和大于第三边判断出a最小为2,再根据二次函数的增减性和对称性判断出对称轴在2、3之间偏向2,即小于2.5,然后列出不等式求解即可.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案【题目】已知2014年3月份在某医院出生的20名新生婴儿的体重如下(单位:kg)
4.7 2.9 3.2 3.5 3.8 3.4 2.8 3.3 4.0 4.5
3.6 4.8 4.3 3.6 3.4 3.5 3.6 3.5 3.7 3.7
(1)求这组数据的极差;
(2)若以0.4kg为组距,对这组数据进行分组,制作了如下的“某医院2014年3月份20名新生婴儿体重的频数分布表”(部分空格未填),请在频数分布表的空格中填写相关的量
某医院2014年3月份20名新生儿体重的频数分布表
组别(kg) | 划记 | 频数 |
略 | ||
略 | ||
3.55﹣3.95 | 正一 | 6 |
略 | ||
略 | ||
略 | ||
合计 | 20 | |
(3)经检测,这20名婴儿的血型的扇形统计图如图所示(不完整),求:
①这20名婴儿中是A型血的人数;
②表示O型血的扇形的圆心角度数.