题目内容
【题目】如图,在平面直角坐标系中,点A的坐标为(﹣2,0),等边△AOC经过平移或轴对称或旋转都可以得到△OBD. 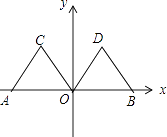
(1)△AOC沿x轴向右平移得到△OBD,则平移的距离是个单位长度;△AOC与△BOD关于直线对称,则对称轴是;△AOC绕原点O顺时针旋转得到△DOB,则旋转角度可以是度.
(2)连接AD,交OC于点E,求AD的长.
【答案】
(1)2;y轴;120
(2)解:如图,连接AD,
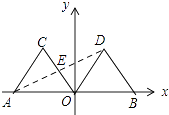
由AO=DO,∠BOD=60°可得,∠OAD=∠ODA=30°,
∴∠ADB=30°+60°=90°,
∴直角三角形ADB中,AD= ![]() =
= ![]() =2
=2 ![]() .
.
【解析】解:(1)△AOC沿x轴向右平移得到△OBD,根据AO=2可知,平移的距离是2个单位长度; △AOC与△BOD关于直线对称,根据线段AB被y轴垂直平分可知,对称轴是y轴;
△AOC绕原点O顺时针旋转得到△DOB,根据∠BOC=120°可知,旋转角度可以是120°;
所以答案是:2;y轴;120
【考点精析】本题主要考查了等边三角形的性质和坐标与图形变化-对称的相关知识点,需要掌握等边三角形的三个角都相等并且每个角都是60°;关于x轴对称的点的特征:两个点关于x轴对称时,它们的坐标中,x相等,y的符号相反,即点P(x,y)关于x轴的对称点为P’(x,-y);关于y轴对称的点的特征:两个点关于y轴对称时,它们的坐标中,y相等,x的符号相反,即点P(x,y)关于y轴的对称点为P’(-x,y)才能正确解答此题.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目