ЬтФПФкШн
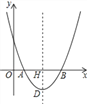
ЁОЬтФПЁПвбжЊЪ§жсЩЯЕФAЁЂBСНЕуЗжБ№ЖдгІЪ§зжaЁЂbЃЌЧвaЁЂbТњзу|4a-b|+ЃЈa-4ЃЉ2=0
![]()
ЃЈ1ЃЉa= ЃЌb= ЃЌВЂдкЪ§жсЩЯУцГіAЁЂBСНЕуЃЛ
ЃЈ2ЃЉШєЕуPДгЕуAГіЗЂЃЌвдУПУы3ИіЕЅЮЛГЄЖШЯђxжсе§АыжсдЫЖЏЃЌЧѓдЫЖЏЪБМфЮЊЖрЩйЪБЃЌЕуPЕНЕуAЕФОрРыЪЧЕуPЕНЕуBОрРыЕФ2БЖЃЛ
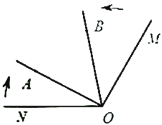
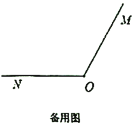
ЃЈ3ЃЉЪ§жсЩЯЛЙгавЛЕуCЕФзјБъЮЊ30ЃЌШєЕуPКЭЕуQЭЌЪБДгЕуAКЭЕуBГіЗЂЃЌЗжБ№вдУПУы3ИіЕЅЮЛГЄЖШКЭУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђCЕудЫЖЏЃЌPЕуЕНДяCЕуКѓЃЌдйСЂПЬвдЭЌбљЕФЫйЖШЗЕЛиЃЌдЫЖЏЕНжеЕуAЃЎЧѓЕуPКЭЕуQдЫЖЏЖрЩйУыЪБЃЌPЁЂQСНЕужЎМфЕФОрРыЮЊ4ЃЌВЂЧѓДЫЪБЕуQЖдгІЕФЪ§ЃЎ
ЁОД№АИЁПЃЈ1ЃЉ4ЃЌ16ЃЎЛЭММћНтЮіЃЛЃЈ2ЃЉ![]() Лђ8УыЃЛЃЈ3ЃЉЕуPКЭЕуQдЫЖЏ4Лђ8Лђ9Лђ11УыЪБЃЌPЃЌQСНЕужЎМфЕФОрРыЮЊ4ЃЎДЫЪБЕуQБэЪОЕФЪ§ЮЊ20ЃЌ24ЃЌ25ЃЌ27ЃЎ
Лђ8УыЃЛЃЈ3ЃЉЕуPКЭЕуQдЫЖЏ4Лђ8Лђ9Лђ11УыЪБЃЌPЃЌQСНЕужЎМфЕФОрРыЮЊ4ЃЎДЫЪБЕуQБэЪОЕФЪ§ЮЊ20ЃЌ24ЃЌ25ЃЌ27ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЗЧИКЪ§ЕФаджЪЧѓГіaЁЂbЕФжЕМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉЙЙНЈЗНГЬМДПЩНтОіЮЪЬтЃЛ
ЃЈ3ЃЉЗжЫФжжЧщаЮЙЙНЈЗНГЬМДПЩНтОіЮЪЬт.
ЃЈ1ЃЉЁпaЃЌbТњзу|4a-b|+ЃЈa-4ЃЉ2Ём0ЃЌ
Ёрa=4ЃЌb=16ЃЌ
ЙЪД№АИЮЊ4ЃЌ16ЃЎ
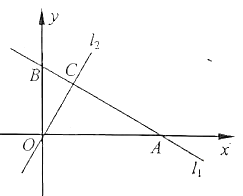
ЕуAЁЂBЕФЮЛжУШчЭМЫљЪОЃЎ
![]()
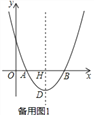
ЃЈ2ЃЉЩшдЫЖЏЪБМфЮЊtsЃЎ
гЩЬтвтЃК3t=2ЃЈ16-4-3tЃЉЛђ3t=2ЃЈ4+3t-16ЃЉЃЌ
НтЕУt=![]() Лђ8ЃЌ
Лђ8ЃЌ
ЁрдЫЖЏЪБМфЮЊ![]() Лђ8УыЪБЃЌЕуPЕНЕуAЕФОрРыЪЧЕуPЕНЕуBЕФОрРыЕФ2БЖЃЛ
Лђ8УыЪБЃЌЕуPЕНЕуAЕФОрРыЪЧЕуPЕНЕуBЕФОрРыЕФ2БЖЃЛ
ЃЈ3ЃЉЩшдЫЖЏЪБМфЮЊtsЃЎ
гЩЬтвтЃК12+t-3t=4Лђ3t-ЃЈ12+tЃЉ=4Лђ12+t+4+3t=52Лђ12+t+3t-4=52ЃЌ
НтЕУt=4Лђ8Лђ9Лђ11ЃЌ
ЁрЕуPКЭЕуQдЫЖЏ4Лђ8Лђ9Лђ11УыЪБЃЌPЃЌQСНЕужЎМфЕФОрРыЮЊ4ЃЎ
ДЫЪБЕуQБэЪОЕФЪ§ЮЊ20ЃЌ24ЃЌ25ЃЌ27ЃЎ

 УЯНЈЦНУћаЃПМОэЯЕСаД№АИ
УЯНЈЦНУћаЃПМОэЯЕСаД№АИ