题目内容
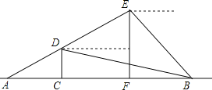
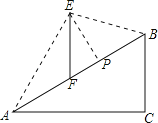
【题目】如图，在坡度i＝1：
的斜坡AB上立有一电线杆EF，工程师在点A处测得E的仰角为60°，沿斜坡前进20米到达B，此时测得点E的仰角为15°，现要在斜坡AB上找一点P，在P处安装一根拉绳PE来固定电线杆，以使EF保持竖直，为使拉绳PE最短，则FP的长度约为_____．（参考数据：
＝1.414，＝1.732）
【答案】
【解析】
要使点E到AB的距离最短，则EP⊥AB，根据题目中的信息可以求得FP的长度，本题得以解决．
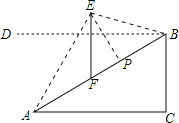
解：作BD∥AC，如右图所示，
∵斜坡AB的坡度i＝1：
，
∴tan∠BAC＝
，
∴∠BAC＝30°，
∵∠EAC＝60°，
∴∠EAF＝30°，
∵要使点E到AB的距离最短，
∴EP⊥AB于点P，
∴tan∠EAP＝
，
∴AP＝
，
∵∠EBD＝15°，BD∥AC，
∴∠DBA＝∠BAC＝30°，
∴∠EBP＝45°，
∴EP＝PB，
∵AP+PB＝AB＝20米，
∴，+EP＝20，
解得，EP＝10﹣10，
又∵EF∥BC，∠B＝90°﹣∠BAC＝60°，
∴∠EFP＝60°，
∵tan∠EFP＝
，
即tan60°＝
，
解得，PF≈4.2米，
故答案为：4.2.
练习册系列答案
相关题目
