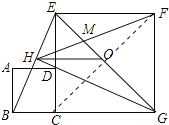
题目内容
【题目】如图，正方形ABCD的边与正方形CGFE的边CE重合，O是EG的中点，
的平分线GH过点D，交BE于点H，连接OH、FH，EG与FH交于点M，对于下面四个结论：①
；②
//且=
；③
；④
∽
，其中正确的有（ ）
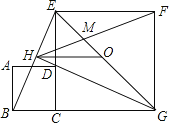
A.1个B.2个C. 3个D.4个
【答案】C
【解析】
由题意分别根据全等三角形的判定与性质和角平分线的性质以及正方形的性质和相似三角形的判定进行综合分析判断求解.
解：
四边形ABCD和四边形CGFE是正方形，
，
，
，
在
和
中，
，
≌
，
，
，
，
，
．
故
正确；
是
的平分线，
，
在
和
中，
，
≌
，
，
又
是EG的中点，
是
的中位线，
，
，
故
正确；
当
时，根据射影定理可得
，
但由题意得：
，
因此错误；
连接CF，如图所示：由得
是直角三角形，
为EG的中点，
，
点H在正方形CGFE的外接圆上，
，
，
，
，
又
，
∽
．
故正确，
故选：C．
练习册系列答案
阅读快车系列答案
相关题目
【题目】某小型加工厂准备每天生产甲、乙两种类型的产品共1000件，原料成本、销售单价，及工人计件工资如表：
甲（元/件） | 乙（元/件） | |
原料成本 | 10 | 8 |
销售单价 | 20 | 16 |
计件工资 | 2 | 1.5 |
设该加工厂每天生产甲型产品x件，每天获得总利润为y元．
（1）求出y与x之间的函数关系式；
（2）若该工厂每天投人总成本不超过10750元，怎样安排甲、乙两种类型的生产量，可使该厂每天所获得的利润最大？并求出最大利润．（总成本＝原料成本+计件工资，利润＝销售收入一投人总成本）
