题目内容
【题目】如图,已知抛物线C1:y=![]() x2﹣2x﹣
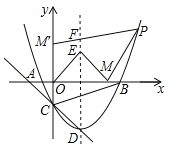
x2﹣2x﹣![]() ,与x轴相交于A、B两点(点A在点B的左边),与y轴交于点C,已知M(4,0),点P是抛物线上的点,其横坐标为6,点D为抛物线的顶点.
,与x轴相交于A、B两点(点A在点B的左边),与y轴交于点C,已知M(4,0),点P是抛物线上的点,其横坐标为6,点D为抛物线的顶点.
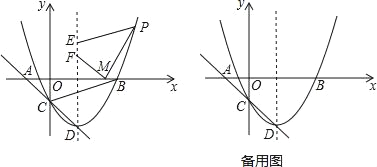
(1)求S△ABC.
(2)点E、F是抛物线对称轴上的两动点,且已知E(2,a+![]() )、F(2,a),当a为何值时,四边形PEFM周长最小?并说明理由.
)、F(2,a),当a为何值时,四边形PEFM周长最小?并说明理由.
(3)将抛物线C1绕点D旋转180°后得到抛物线C2沿直线CD平移,平移后的抛物线交y轴于点Q,顶点为R,平移后是否存在这样的抛物线,使△CRQ为等腰三角形?若存在,请求出此时抛物线的解析式;若不存在,请说明理由.
【答案】(1)S=3+![]() ;(2)a=
;(2)a=![]() ;(3)当a=2时,抛物线解析式为y
;(3)当a=2时,抛物线解析式为y![]() (x﹣2)2﹣2
(x﹣2)2﹣2![]() ;当a=﹣2+2
;当a=﹣2+2![]() 时,抛物线解析式为y
时,抛物线解析式为y![]() (x+2﹣2
(x+2﹣2![]() )2+2﹣2
)2+2﹣2![]() .
.
【解析】
(1)对于抛物线C1,令x=0及y=0,分别求出y与x的值,确定出C,A,B坐标,得到AB与OC的长,即可求出三角形ABC面积;
(2)如图所示,作M关于对称轴的对称点O,将点O向上平移![]() 个单位得到M′,连接PM′,与对称轴交于点F,此时四边形PEFM周长最小,求出M′与P坐标,利用待定系数法确定出直线M′P解析式,令x=2求出y的值,即可确定出此时a的值;
个单位得到M′,连接PM′,与对称轴交于点F,此时四边形PEFM周长最小,求出M′与P坐标,利用待定系数法确定出直线M′P解析式,令x=2求出y的值,即可确定出此时a的值;
(3)根据题意,利用旋转性质确定出抛物线C2与直线CD解析式,再利用平移性质确定出抛物线C2平移后的解析式,表示出C,R,Q坐标,进而表示出CR2,CQ2,RQ2,根据CR2=CQ2;CR2=RQ2;CQ2=RQ2,分别求出a的值即可.
(1)对于抛物线C1:y![]() x2﹣2x
x2﹣2x![]() ,令x=0,得到:y
,令x=0,得到:y![]() ,即C(0,
,即C(0,![]() ),令y=0,得到:
),令y=0,得到:![]() x2﹣2x
x2﹣2x![]() 0,解得:x1=1
0,解得:x1=1![]() ,x2=3
,x2=3![]() ,∴A(1
,∴A(1![]() ,0),B(3
,0),B(3![]() ,0),则S
,0),则S![]() [(3
[(3![]() )﹣(1
)﹣(1![]() )]
)]![]() ;
;
(2)如图所示,作M关于对称轴的对称点O,将点O向上平移![]() 个单位得到M′,连接PM′,与对称轴交于点F,此时四边形PEFM周长最小,易得M′(0,
个单位得到M′,连接PM′,与对称轴交于点F,此时四边形PEFM周长最小,易得M′(0,![]() ),P(6,6
),P(6,6![]() ),设直线PM′解析式为y=kx+b,把M′与P坐标代入得:
),设直线PM′解析式为y=kx+b,把M′与P坐标代入得:![]() ,解得:
,解得: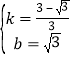 ,∴y
,∴y![]() ,令x=2,得到:y
,令x=2,得到:y![]() ,∴a
,∴a![]() ,解得:a
,解得:a![]() ;
;
(3)易得抛物线C1:y![]() (x﹣2)2﹣2
(x﹣2)2﹣2![]() ,旋转180°后抛物线C2:y
,旋转180°后抛物线C2:y![]() (x﹣2)2﹣2
(x﹣2)2﹣2![]() ,直线CD解析式为y=﹣x
,直线CD解析式为y=﹣x![]() ,设抛物线C2平移后的关系式为y
,设抛物线C2平移后的关系式为y![]() (x﹣a)2﹣a
(x﹣a)2﹣a![]() ,易得C(0,
,易得C(0,![]() ),R(a,﹣a
),R(a,﹣a![]() ),Q(0,
),Q(0,![]() a2﹣a
a2﹣a![]() ),CR2=a2+a2,CQ2=a2(
),CR2=a2+a2,CQ2=a2(![]() a+1)2,RQ2=a2
a+1)2,RQ2=a2![]() a4,分三种情况讨论:
a4,分三种情况讨论:
①当CR2=CQ2时,得到:a2+a2=a2(![]() a+1)2,解得:a=﹣2+2
a+1)2,解得:a=﹣2+2![]() 或a=﹣2﹣2
或a=﹣2﹣2![]() (舍去);
(舍去);
②当CR2=RQ2时,得到:a2+a2=a2![]() a4,解得:a=2或a=﹣2(舍去);
a4,解得:a=2或a=﹣2(舍去);
③当RQ2=CQ2时,得到:a2(![]() a+1)2=a2
a+1)2=a2![]() a4,解得:a=0(舍去).
a4,解得:a=0(舍去).
综上所述:当a=2时,抛物线解析式为y![]() (x﹣2)2﹣2
(x﹣2)2﹣2![]() ;当a=﹣2+2
;当a=﹣2+2![]() 时,抛物线解析式为y
时,抛物线解析式为y![]() (x+2﹣2
(x+2﹣2![]() )2+2﹣2
)2+2﹣2![]() .
.

【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 | ||
高中部 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
【题目】某公司欲招聘一名部门经理,对甲、乙、丙三名候选人进行了三项素质测试.各项测试成绩如表格所示:
测试项目 | 测试成绩 | ||
甲 | 乙 | 丙 | |
专业知识 | 74 | 87 | 90 |
语言能力 | 58 | 74 | 70 |
综合素质 | 87 | 43 | 50 |
(1)如果根据三次测试的平均成绩确定人选,那么谁将被录用?
(2)根据实际需要,公司将专业知识、语言能力和综合素质三项测试得分按4:3:1的比例确定每个人的测试总成绩,此时谁将被录用?
(3)请重新设计专业知识、语言能力和综合素质三项测试得分的比例来确定每个人的测试总成绩,使得乙被录用,若重新设计的比例为x:y:1,且x+y+1=10,则x= ,y= .(写出x与y的一组整数值即可).