��Ŀ����
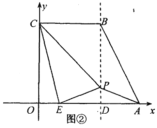
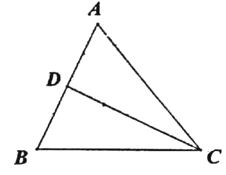
����Ŀ����ͼ,�ڡ�ABC��.AC=BC=5.AB=6.CD��AB������.��P�ӵ�C��������ÿ��2.5����λ���ȵ��ٶ���C-D-C�˶�.�ڵ�P������ͬʱ����QҲ�ӵ�C��������ÿ��2����λ���ȵ��ٶ��ر�CA���A�˶�.��һ����ֹͣ�˶�ʱ����һ����Ҳ��ֹ֮ͣ�����P�˶���ʱ��Ϊt��.
��1���ú�t�Ĵ���ʽ��ʾCP��CQ�ij���.
��2���ú�t�Ĵ���ʽ��ʾ��CPQ�����.
��3������CPQ���CAD����ʱ��ֱ��д��t��ȡֵ��Χ.
���𰸡���1����0��t��![]() ʱ��CP=2.5t��CQ=2t����
ʱ��CP=2.5t��CQ=2t����![]() ʱ��CP=8-2.5t��CQ=2t��
ʱ��CP=8-2.5t��CQ=2t��
��2����0��t��![]() ʱ��S��CPQ=
ʱ��S��CPQ=![]() PCsin��ACDCQ=
PCsin��ACDCQ=![]() ��2.5t��
��2.5t��![]() ��2t=
��2t=![]() ����
����![]() ʱ��S��CPQ=
ʱ��S��CPQ=![]() PCsin��ACDCQ=
PCsin��ACDCQ=![]() ����8-2.5t����
����8-2.5t����![]() ��2t=
��2t=![]() .
.
��3��0��t��![]() ��
��![]() s
s
��������
��1�����������Σ���0��t��![]() ʱ����
ʱ����![]() ��t
��t![]() ʱ���ֱ���⼴�ɣ�
ʱ���ֱ���⼴�ɣ�
��2�����������Σ���0��t��![]() ʱ����
ʱ����![]() ��t��
��t��![]() ʱ������S��CPQ=
ʱ������S��CPQ=![]() PCsin��ACDCQ�ֱ���⼴�ɣ�
PCsin��ACDCQ�ֱ���⼴�ɣ�
��3�����������Σ���0��t��![]() ������֤����QCP�ס�DCA����
������֤����QCP�ס�DCA����![]() ��t
��t![]() ����QPC=90��ʱ����QPC�ס�ADC������������⼴�ɣ�
����QPC=90��ʱ����QPC�ס�ADC������������⼴�ɣ�
�⣺��1����CA=CB��AD=BD=3��
��CD��AB��
���ADC=90����
��CD=![]() =
=![]() =4��
=4��
��0��t��![]() ʱ��CP=2.5t��CQ=2t��
ʱ��CP=2.5t��CQ=2t��
��![]() ʱ��CP=8-2.5t��CQ=2t��
ʱ��CP=8-2.5t��CQ=2t��
��2����sin��ACD=![]() =
=![]() ��
��
�൱0��t��![]() ʱ��S��CPQ=
ʱ��S��CPQ=![]() PCsin��ACDCQ=
PCsin��ACDCQ=![]() ��2.5t��
��2.5t��![]() ��2t=
��2t=![]()
��![]() ʱ��S��CPQ=
ʱ��S��CPQ=![]() PCsin��ACDCQ=
PCsin��ACDCQ=![]() ����8-2.5t����
����8-2.5t����![]() ��2t=
��2t=![]() .
.
��3���ٵ�0��t��![]() ʱ��
ʱ��
��CP=2.5t��CQ=2t��
��![]() =
=![]() ��
��
��![]() =
=![]() ��
��
��![]() ��
��
�ߡ�PCQ=��ACD��
���QCP�ס�DCA��
��0��t��![]() ʱ����QCP�ס�DCA��
ʱ����QCP�ס�DCA��
�ڵ�![]() ʱ������
ʱ������
��![]() ��
��
��![]() ��
��
��ã�![]() ��
��
��������������������t��ֵΪ��0��t��![]() ��
��![]() sʱ����QCP�ס�DCA��
sʱ����QCP�ס�DCA��

 ������ѧ���̲���ȫ���ϵ�д�
������ѧ���̲���ȫ���ϵ�д�����Ŀ���������Ϊ�Ӽס��������˶�Ա��ѡ��һ�˲μ�ʡ�����������ǽ��������β��ԣ����Գɼ����±�����λ��������
��һ�� | �ڶ��� | ������ | ���Ĵ� | ����� | ������ | |
�� | 10 | 8 | 9 | 8 | 10 | 9 |
�� | 10 | 7 | 10 | 10 | 9 | 8 |
��1�����ݱ����е����ݣ��ֱ����ס��ҵ�ƽ���ɼ���
��2���ֱ����ס������β��Գɼ��ķ��
��3�����ݣ�1������2������Ľ��������Ϊ�Ƽ�˭�μ�ʡ���������ʣ���˵������.