题目内容
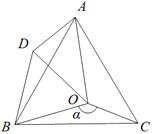
【题目】如图,点O是等边△ABC内一点,∠BOC=![]() ,∠AOC=100°,将△BOC绕点B按逆时针方向旋转60°得到△BDA,连接OD.
,∠AOC=100°,将△BOC绕点B按逆时针方向旋转60°得到△BDA,连接OD.
(1) 求证:△BOD是等边三角形.
(2) 当![]() =150°时,试判断△AOD的形状,并说明理由.
=150°时,试判断△AOD的形状,并说明理由.
(3) 若△AOD是等腰三角形,请你直接写出![]() 的度数.
的度数.
【答案】(1)证明见解析;(2)α=150°时,△AOD是直角三角形;理由见解析;(3)130°或100°或160°
【解析】
(1)根据旋转的性质可得出OB=BD,∠OBD=60°,根据等边三角形的判定即可求证;
(2)由(1)的结论可得∠BDO=60°;由于α=150°,所以∠ADB=∠BOC=150°,继而可得∠ADO=∠ADB-∠ODB=90°,由∠AOC=100°,∠BOD=60°,可求出∠AOD=360°-∠α-∠AOC-∠COD=360°-150°-100°-60°=50°,根据三角形的内角即可判定三角形的形状;
(3)分AO=AD、AO=OD、DO=AD三种情况,根据等腰三角形的概念,三角形内角和定理计算.
(1)证明:∵将△BOC绕点B按逆时针方向旋转60°得△BDA,
∴BO=BD,∠OBD=60°,
∴△BOD是等边三角形.
(2)解:当α=150°时,△AOD是直角三角形.理由是:
∵将△BOC绕点B按逆时针方向旋转60°得△BDA,
∴△BOC≌△BDA,
∴∠ADB=∠BOC=150°,
又∵△BOD是等边三角形,
∴∠ODB=60°,
∴∠ADO=∠ADB-∠ODB=90°,
∵∠α=150°,∠AOC=100°,∠BOD=60°,
∴∠AOD=360°-∠α-∠AOC-∠COD=360°-150°-100°-60°=50°,
∴△AOD不是等腰直角三角形,
即△AOD是直角三角形.
(3) ∵△BOD是等边三角形,
∴∠ADO=α-60°,
∵OD=OA,
∴∠OAD=∠ODA=α-60°,
∴∠AOD=180°-2(α-60°),解得α=100°;
当OD=AD时,α+100°+60°+∠AOD=360°,
∠AOD=![]() ,解得α=160°;
,解得α=160°;
当OA=AD时,α+100°+60°+∠AOD=360°,∠AOD=α-60°,解得,α=130°
综合可得:130°或100°或160°

 中考解读考点精练系列答案
中考解读考点精练系列答案