Question

【题目】（1）如图，点C、D在线段AB上，D是线段AB的中点，AC=AD ，CD=4 ，求线段AB的长．

（2）如图，点O是直线AB上的一点，OD是∠AOC的平分线，OE是∠COB的平分线，若∠AOD=14°，求∠DOE、∠BOE的度数．

Answer 1

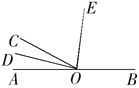
【答案】（1）12；（2）∠DOE=90°，∠BOE=76°．

【解析】

（1）根据ACAD，CD＝4，求出CD与AD，再根据D是线段AB的中点，即可得出答案；

（2）利用角平分线和图中角与角的关系计算即可．

（1）∵ACAD，CD＝4，∴CD＝AD﹣AC＝ADADAD，∴ADCD＝6．

∵D是线段AB的中点，∴AB＝2AD＝12．

（2）∵OD是∠COA的平分线，∠AOD＝14°，∴∠AOC＝2∠AOD＝2×14°＝28°．

∵∠AOB＝180°，∴∠BOE∠BOC（180°﹣∠AOC）＝76°；

∠DOE∠BOC∠AOC＝76°+14°＝90°．

故∠DOE＝90°，∠BOE＝76°．