题目内容
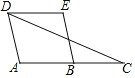
【题目】已知等腰△ABC的顶角∠A=36°（如图）．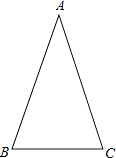 
（1）作底角∠ABC的平分线BD，交AC于点D（用尺规作图，不写作法，但保留作图痕迹，然后用墨水笔加墨）；
（2）通过计算说明△ABD和△BDC都是等腰三角形．
【答案】
（1）解：如图所示：
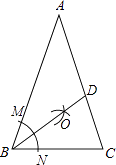
BD即为所求；
（2）解：∵∠A=36°，
∴∠ABC=∠C=（180°﹣36°）÷2=72°，
∵BD平分∠ABC，
∴∠ABD=∠DBC=72°÷2=36°，
∴∠CDB=180°﹣36°﹣72°=72°，
∵∠A=∠ABD=36°，∠C=∠CDB=72°，
∴AD=DB，BD=BC，
∴△ABD和△BDC都是等腰三角形．
【解析】（1）首先以B为圆心，任意长为半径画弧，两弧交AB、BC于M、N两点；再分别以M、N为圆心，大于 
MN长为半径画弧，两弧交于一点O，画射线BO交AC于D．（2）根据三角形内角和为180°计算出∠ABC，∠C，∠CDB，∠ABD，∠DBC的度数，再根据等角对等边可证出结论．
练习册系列答案
相关题目
