题目内容
【题目】如图,四边形![]() 是一张矩形纸片,
是一张矩形纸片,![]() ,把纸片
,把纸片![]() 对折,折痕为
对折,折痕为![]() ,展开后再过点
,展开后再过点![]() 折叠该纸片,使点
折叠该纸片,使点![]() 落在
落在![]() 上的点
上的点![]() 处,且折痕
处,且折痕![]() 与
与![]() 相交于点
相交于点![]() ,再次展平后,连接
,再次展平后,连接![]() ,
,![]() ,并延长
,并延长![]() 交
交![]() 于点
于点![]() .
.
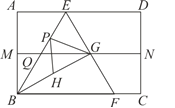
(1)求证:![]() 是等边三角形;
是等边三角形;
(2)求![]() ,
,![]() 的长;
的长;
(3)![]() 为线段
为线段![]() 上一动点,
上一动点,![]() 是
是![]() 的中点,则
的中点,则![]() 的最小值是 .(请直接写出结果)
的最小值是 .(请直接写出结果)
【答案】(1)详见解析;(2)![]() ,
,![]() ;(3)
;(3)![]()
【解析】
(1)连接AG,根据垂直平分线的性质和折叠的性质得出AG=AB=BG,由此得出△ABG为等边三角形,根据等边三角形的性质和三角形内角和定理即可得出△EBF为等边三角形.
(2)设AE=x,则BE=2x,根据勾股定理可求出AE的长度,则BE的长度可求,根据![]() 是等边三角形求出BF的长度,利用三角形中位线即可求出QG的长度;
是等边三角形求出BF的长度,利用三角形中位线即可求出QG的长度;
(3)根据题意可得出M点与H点关于BE所在直线对称,所以P与Q重合时,PH+PG的值最小,最小值为MG的长度,进而问题可解.
(1)如图,连接AG
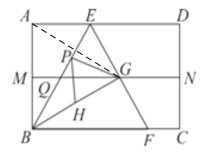
∵MN垂直平分AB
∴AG=BG
根据轴对称的性质,可得
AB=BG,
∴AG=AB=BG.
∴△ABG为等边三角形.
![]()
∴∠ABE=30°,∠AEB=∠GEB=60°
又∵∠EBF=60°
![]()
∴△EBF为等边三角形
(2)由(1)得∠ABE=30°
设AE=x,则BE=2x
∵AB=2,![]()
∴![]()
即![]() ,
,![]()
∵△EBF为等边三角形
![]()
∴![]()
(3)根据条件易知M点与H点关于BE所在直线对称
∴P与Q重合时,PH+PG的值最小
又∵![]() ,
,![]()
∴![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目