题目内容
【题目】在平面内有∠AOB=60°，∠AOC=40°，OD是∠AOB的平分线，OE是∠AOC的平分线，求∠DOE的度数．(请作图解答)
【答案】∠DOE=50°或10°．
【解析】
根据角平分线的定义求得∠AOE和∠AOD的度数即可．
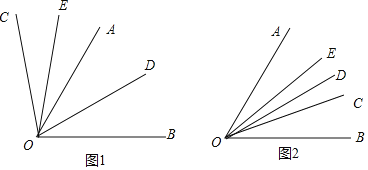
如图1，∵∠AOB=60°，∠AOC=40°，OD是∠AOB的平分线，OE是∠AOC的平分线，
∴∠AOE=
∠AOC=20°，∠AOD=∠AOB=30°，
∴∠DOE=∠AOE+∠AOD=50°，
如图2，∵∠AOB=60°，∠AOC=40°，OD是∠AOB的平分线，OE是∠AOC的平分线，
∴∠AOE=∠AOC=20°，∠AOD=∠AOB=30°，
∴∠DOE=∠AOD-∠AOE=10°，
综上所述，∠DOE=50°或10°．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】已知三角形A1B1C1是由三角形ABC经过平移得到的，其中A、B、C三点的对应点分别是A1、B1、C1，它们在平面直角坐标系中的坐标如表所示：
三角形ABC | A（0，0） | B（﹣1，2） | C（2，5） |
三角形A1B1C1 | A1（a，2） | B1（4，b） | C1（7，7） |
（1）观察表中各对应点坐标的变化，填空a= ，b= ；
（2）在图中的平面直角坐标系中画出三角形ABC及三角形A1B1C1；
（3）P（m，n）为三角形ABC中任意一点，则平移后对应点P'的坐标为 ．
