题目内容
如图,在平面直角坐标系 中,已知点
中,已知点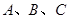 在双曲线
在双曲线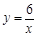 上,
上, 轴于D,
轴于D, 轴于
轴于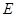 ,点
,点 在
在 轴上,且
轴上,且 ,则图中阴影部分的面积之和为
,则图中阴影部分的面积之和为
| A.6 | B.12 | C.18 | D.24 |
B
解析试题分析:过A作AG垂直于x轴,交x轴于点G,由AO=AF,利用三线合一得到G为OF的中点,根据等底同高得到三角形AOD的面积等于三角形AFD的面积,再由A,B及C三点都在反比例函数图象上,根据反比例的性质得到三角形BOD,三角形COE及三角形AOG的面积都相等,都为 ,由反比例解析式中的k值代入,求出三个三角形的面积,根据阴影部分的面积等于三角形BOD的面积+三角形COE的面积+三角形AOG的面积+三角形AFG的面积=4三角形AOD的面积,即为2|k|,即可得到阴影部分的面积之和.
,由反比例解析式中的k值代入,求出三个三角形的面积,根据阴影部分的面积等于三角形BOD的面积+三角形COE的面积+三角形AOG的面积+三角形AFG的面积=4三角形AOD的面积,即为2|k|,即可得到阴影部分的面积之和.
解:过A作AG⊥x轴,交x轴于点G
∵AO=AF,AG⊥OF,
∴G为OF的中点,即OG=FG,
∴S△OAG=S△FAG,
又A,B及C点都在反比例函数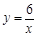 上,
上,
∴S△OAG=S△BOD=S△COE= =3,
=3,
∴S△OAG=S△BOD=S△COE=S△FAG=3,
则S阴影=S△OAG+S△BOD+S△COE+S△FAG=12,
故选B.
考点:反比例函数的性质,等腰三角形的性质,三角形的面积公式
点评:反比例函数 (k≠0)图象上的点到坐标轴的垂线,此点到原点的连线及坐标轴围成的直角三角形的面积等于
(k≠0)图象上的点到坐标轴的垂线,此点到原点的连线及坐标轴围成的直角三角形的面积等于 ,熟练掌握此性质是解本题的关键.
,熟练掌握此性质是解本题的关键.

练习册系列答案
相关题目
已知k1<0<k2,则函数 和
和 的图象大致是
的图象大致是
A. | B. | C. | D. |
如图,直线y=mx与双曲线 交于A,B两点,过点A作AM⊥x轴,垂足为点M,连接BM,若S△ABM=2,则k的值为
交于A,B两点,过点A作AM⊥x轴,垂足为点M,连接BM,若S△ABM=2,则k的值为
| A.﹣2 | B.2 | C.4 | D.﹣4 |
反比例函数 的图象如图所示,则当x>1时,函数值y的取值范围是( )
的图象如图所示,则当x>1时,函数值y的取值范围是( )
| A.y>1 | B.0<y<1 | C.y<2 | D.0<y<2 |
某厂现有300吨煤,这些煤能烧的天数y与平均每天烧的吨数x之间的函数关系是( )
A.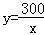 (x>0) (x>0) | B.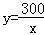 (x≥0) (x≥0) |
| C.y=300x(x≥0) | D.y=300x(x>0) |
 的图象上,直角边BC在x轴上,∠ABC=90°,∠ACB=30°,OC=4,连接OA,∠AOB=60°,则k的值是
的图象上,直角边BC在x轴上,∠ABC=90°,∠ACB=30°,OC=4,连接OA,∠AOB=60°,则k的值是





 在双曲线
在双曲线 上,若
上,若 ,则
,则
 (用“>”或“<”或“=”号表示).
(用“>”或“<”或“=”号表示).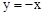 与函数
与函数 的图象相交于A,B两点,过A,B两点分别作y轴的垂线,垂足分别为点C,D.则四边形ACBD的面积为
的图象相交于A,B两点,过A,B两点分别作y轴的垂线,垂足分别为点C,D.则四边形ACBD的面积为