Question

【题目】如图所示，从点O发出四条射线OA，OB，OC，OD，已知∠AOC＝∠BOD＝90°.

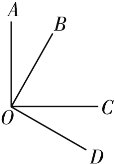
(1)若∠BOC＝35°，则∠AOB= ，∠COD= ;

(2)若∠BOC＝46°，则∠AOB= ，∠COD= .

(3)你发现了什么？你能说明其中的道理吗？

Answer 1

【答案】(1)∠AOB＝55°，∠COD＝55°.(2)∠AOB＝44°，∠COD＝44°. (3)∠AOB＝∠COD

【解析】

（1）、（2）根据余角和补角的定义可直接得出结论；（3）根据（1）、（2）的计算及等式的性质可得出结论．

解：(1)∵∠AOC＝∠BOD＝90°.

∴∠AOB＝90°-∠BOC=55°，∠COD＝90°-∠BOC=55°.

(2) ∵∠AOC＝∠BOD＝90°.

∴∠AOB＝90°-∠BOC=44°，∠COD＝90°-∠BOC=44°.

(3)∠AOB＝∠COD，

因为∠AOB＋∠BOC＝90°，∠COD＋∠BOC＝90°，

又因为∠BOC＝∠BOC，

所以∠AOB＝∠COD.