题目内容
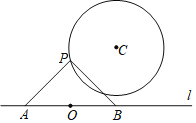
【题目】如图,已知⊙C的半径为2,圆外一点O满足OC=3.5,点P为⊙C上一动点,经过点O的直线l上有两点A、B,且OA=OB,∠APB=90°,l不经过点C,则AB的最小值为( )
A. 2 B. 2.5 C. 3 D. 3.5
【答案】C
【解析】
先连接OP,PC,OC,根据OP+PC≥OC,OC=3.5,PC=2,即可得到当点O,P,C三点共线时,OP最短,依据OA=OB,∠APB=90°,可得点P在以O为圆心,AB为直径的圆上,进而得到⊙O与⊙C相切时,OP最短,根据OP=3.5-2=1.5,可得AB=2OP=3.
解:如图,连接OP,PC,OC,
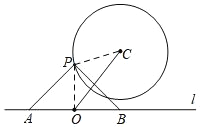
∵OP+PCOC,OC=3.5,PC=2,
∴当点O,P,C三点共线时,OP最短,
如图,∵OA=OB,∠APB=90°,
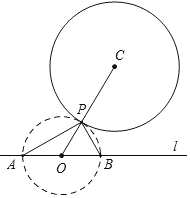
∴点P在以O为圆心,AB为直径的圆上,
∴⊙O与⊙C相切时,OP最短,
∵OC=3.5, PC=2,
∴OP=3.53=1.5,
∴AB=2OP=3.
故选C.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案【题目】某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了15人某月的加工零件个数:
每人加工件数 | 540 | 450 | 300 | 240 | 210 | 120 |
人数 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)写出这15人该月加工零件数的平均数、中位数和众数。
(2)若以本次统计所得的月加工零件数的平均数定为每位工人每月的生产定额,你认为这个定额是否合理,为什么?
【题目】某商店购进一种商品,每件商品进价30元.试销中发现这种商品每天的销售量y(件)
与每件销售价x(元)的关系数据如下:
x | 30 | 32 | 34 | 36 |
y | 40 | 36 | 32 | 28 |
(1)已知y与x满足一次函数关系,根据上表,求出y与x之间的关系式(不写出自变量x的取值范围);
(2)如果商店销售这种商品,每天要获得150元利润,那么每件商品的销售价应定为多少元?
(3)设该商店每天销售这种商品所获利润为w(元),求出w与x之间的关系式,并求出每件商品销售价定为多少元时利润最大?