��Ŀ����
����Ŀ��ij��˾Ӫ��![]() ���ֲ�Ʒ�������г����У�ȷ��������Ϣ��
���ֲ�Ʒ�������г����У�ȷ��������Ϣ��
��Ϣ1������![]() �ֲ�Ʒ��������
�ֲ�Ʒ��������![]() (��Ԫ)�������۲�Ʒ
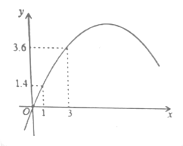
(��Ԫ)�������۲�Ʒ![]() (��)֮����ڶ��κ�����ϵ����ͼ��ʾ
(��)֮����ڶ��κ�����ϵ����ͼ��ʾ
��Ϣ2������![]() �ֲ�Ʒ��������
�ֲ�Ʒ��������![]() (��Ԫ)�����۲�Ʒ
(��Ԫ)�����۲�Ʒ![]() (��)֮�����������������ϵ
(��)֮�����������������ϵ![]()
����������Ϣ������������⣺
��1������κ����ı���ʽ��
��2���ù�˾������![]() ���ֲ�Ʒ��10�֣������һ��Ӫ������ʹ����
���ֲ�Ʒ��10�֣������һ��Ӫ������ʹ����![]() ���ֲ�Ʒ��õ�����֮�������������Ƕ�����Ԫ?
���ֲ�Ʒ��õ�����֮�������������Ƕ�����Ԫ?
���𰸡���1��![]() ����2������A��Ʒ6�֣�����B��Ʒ4�֣�����֮��������Ϊ6.6��Ԫ
����2������A��Ʒ6�֣�����B��Ʒ4�֣�����֮��������Ϊ6.6��Ԫ
��������
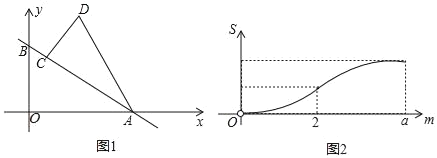
(1)�������߹�ԭ�����y��x��ĺ�����ϵʽΪy=ax2+bx+c�������ô���ϵ�������ɵã�
(2)�蹺��A��Ʒm�֣�����B��Ʒ(10m)�֣�����A��B���ֲ�Ʒ��õ�����֮��ΪWԪ�����ݣ�A��Ʒ����+B��Ʒ����=������ɵ�W=0.1m2+1.5m+0.3(10m)���䷽����ݶ��κ��������ʼ���֪��ֵ�����
�⣺(1)����κ����ı���ʽΪy=ax2+bx+c��
��ͼ�������߹���(0,0)��(1,1.4)��(3,3.6)��
�����������������ʽ��
��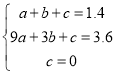 ,
,
���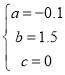
���Զ��κ����ı���ʽΪy=0.1x2+1.5x��
(2)�蹺��A��Ʒm�֣�����B��Ʒ(10m)�֣�����A��B���ֲ�Ʒ��õ�����֮��ΪWԪ��
��W=0.1m2+1.5m+0.3(10m)��
=0.1m2+1.2m+3��
=0.1(m6)2+6.6��
��0.1<0��
��൱m=6ʱ��Wȡ�����ֵ�����ֵΪ6.6��Ԫ��
�𣺹���A��Ʒ6�֣�����B��Ʒ4�֣�����A��B���ֲ�Ʒ��õ�����֮��������������6.6��Ԫ��