题目内容
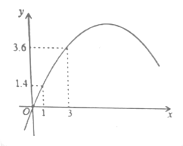
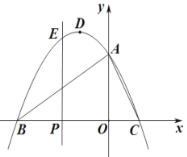
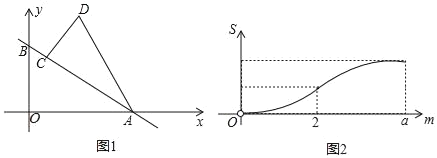
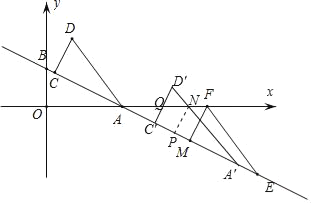
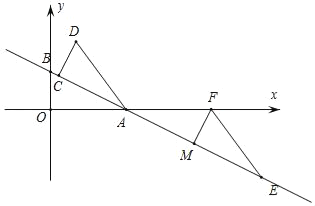
【题目】如图1,直线y=kx+1与x轴、y轴分别相交于点A、B,将△AOB绕点A顺时针旋转,使AO落在AB上,得到△ACD,将△ACD沿射线BA平移,当点D到达x轴时运动停止.设平移距离为m,平移后的图形在x轴下方部分的面积为S,S关于m的函数图象如图2所示(其中0<m≤2,2<m≤a时,函数的解析式不同)
(1)填空:a= ,k= ;
(2)求S关于m的解析式,并写出m的取值范围.
【答案】(1)a=4, k=﹣![]() ;(2)S=
;(2)S=![]() (0<m≤2)或S=﹣
(0<m≤2)或S=﹣![]() +m﹣1(2<m≤4)
+m﹣1(2<m≤4)
【解析】
(1)先由函数图象变化的特点,得出m=2时的变化是三角形C点与A点重合时,从而得AC的值,进而得点A坐标,易求得点B坐标,从而问题易解得;
(2)当0<m≤2时,平移后的图形在x轴下方部分为图中△AA′N;2<m≤4时,平移后的图形在x轴下方部分的面积S为三角形ANA′的面积减去三角形AQC的面积.
(1)从图2看,m=2时的变化是三角形C点与A点重合时,
∴AC=2,
又∵OA=AC
∴A(2,0),
∴k=﹣![]() ,
,
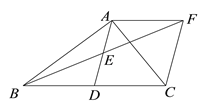
由平移性质可知:∠FEM=∠FAM=∠DAC=∠BAO,
从图中可知△EFM≌△AFM(AAS)
∴AM=EM,
∴AM=2,
∴a=4;
(2)当0<m≤2时,平移后的图形在x轴下方部分为图中△AA′N,则AA′=m,翻折及平移知,
∠NAA′=∠NA′A,
∴NA=NA′,
过点N作NP⊥AA′于点P,则AP=A′P=![]() ,
,
由(1)知,OB=1,OA=2,则tan∠OAB=![]() ,
,
则tan∠NAA′=![]() ,
,
∴NP=![]() =
=![]() ,
,
∴S=![]() ×AA′×NP=
×AA′×NP=![]() ×m×
×m×![]() =
=![]()
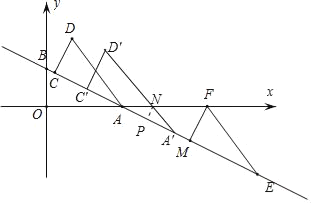
2<m≤4时,如下图所示,可知CC′=m,AC′=m﹣2,AA′=m,
同上可分别求得则AP=A′P=![]() ,NP=
,NP=![]() =
=![]() ,C′Q=
,C′Q=![]()
∴S=S△AA′N﹣S△AQC′=![]() ﹣
﹣![]() (m﹣2)×
(m﹣2)×![]() =﹣
=﹣![]() +m﹣1
+m﹣1
综上,S关于m的解析式为:S=![]() (0<m≤2)或S=﹣
(0<m≤2)或S=﹣![]() +m﹣1(2<m≤4)
+m﹣1(2<m≤4)

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
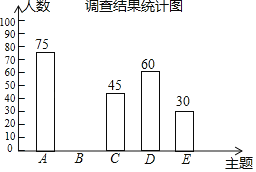
英才计划同步课时高效训练系列答案【题目】2019年3月19日,河南省教育厅发布《关于推进中小学生研学旅行的实施方案》,某中学为落实方案,给学生提供了以下五种主题式研学线路:A.“红色河南”,B.“厚重河南”C.“出彩河南”,D.“生态河南”,E.“老家河南”为了解学生最喜欢哪一种研学线路(每人只选取一种),随机抽取了部分学生进行调查,将调查结果绘制成如下不完整的统计表和统计图.根据以上信息解答下列问题:
调查结果统计表
主题 | 人数/人 | 百分比 |
A | 75 | n% |
B | m | 30% |
C | 45 | 15% |
D | 60 | |
E | 30 |
(1)本次接受调查的总人数为 人,统计表中m= ,n= .
(2)补全条形统计图.
(3)若把条形统计图改为扇形统计图,则“生态河南”主题线路所在扇形的圆心角度是 .
(4)若该实验中学共有学生3000人,请据此估计该校最喜欢“老家河南”主题线路的学生有多少人.