题目内容
【题目】如图,在![]() 中,
中,![]() 、
、![]() 的角平分线相交于点
的角平分线相交于点![]() ,①若
,①若![]() ,则
,则![]() __________,②若
__________,②若![]() ,
,![]() ,则
,则![]() ___________.
___________.

【答案】110° 70°
【解析】
①先根据三角形内角和求出∠BAC+∠BCA=140°,再根据角平分线的定义求出∠IAC+∠ICA的值,然后利用三角形内角和即可求解;
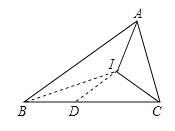
②在BC上取CD=AC,连接BI、DI,利用SAS证明△ACI与△DCI全等,可得AI=DI,∠CAI=∠CDI,再根据BC=AI+AC求出AI=BD,从而可得BD=DI,由三角形外角的性质可得∠CDI=2∠DBI,再根据角平分线的定义即可求出∠CDI=∠ABC,又∠BAC=2∠CAI,代入数据进行计算即可求解;
①∵![]() ,
,
∴∠BAC+∠BCA=140°,
∵AI、CI分别是![]() 、
、![]() 的角平分线,
的角平分线,
∴∠IAC+∠ICA=![]() (∠BAC+∠BCA)=70°,
(∠BAC+∠BCA)=70°,
∴∠AIC=180°-70°=110°;
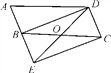
②如图1,在BC上取CD=AC,连接BI、DI,
∵CI平分∠ACB,
∴∠ACI=∠BCI,
在△ACI与△DCI中,
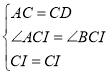 ,
,
∴△ACI≌△DCI(SAS),
∴AI=DI,∠CAI=∠CDI,
∵BC=AI+AC,
∴BD=AI,
∴BD=DI,
∴∠IBD=∠BID,
∴∠CDI=∠IBD+∠BID=2∠IBD,
又∵AI、CI分别是∠BAC、∠ACB的平分线,
∴BI是∠ABC的平分线,
∴∠ABC=2∠IBD,∠BAC=2∠CAI,
∴∠CDI=∠ABC,
∴∠BAC=2∠CAI=2∠CDI=2∠ABC,
∵∠ABC=35°,
∴∠BAC=35°×2=70°.

练习册系列答案
相关题目