Question

【题目】若两个二次函数的图象的顶点、开口方向都相同，则称这两个二次函数为“同类二次函数”．

（1）请直接写出两个为“同类二次函数”的函数；

（2）已知关于x的二次函数y1＝（x+2）2﹣3和y2＝ax2+bx﹣1，若y1+y2与y1为“同类二次函数”，求函数y2的表达式，并求出当﹣3≤x≤0时，y2的最大值．

Answer 1

【答案】（1）它们是“同类二次函数”；（2）函数y2的表达式为y2＝﹣x2﹣x﹣1，当﹣3≤x≤0时，y2的最大值为0．

【解析】

（1）根据“同类二次函数”的定义即可写出；
（2）根据y1+y2与y1为“同类二次函数”，列式即可求函数y2的表达式，再根据函数y2的表达式即可求解．

（1）根据“同类二次函数”的定义可知：

y＝2（x﹣1）2+4和y＝（x﹣1）2+4

顶点坐标都是（1，4），开口方向都向上，

所以它们是“同类二次函数”；

（2）根据题意，得

y1+y2＝（x+2）2﹣3+ax2+bx﹣1，

＝（1+a）x2+（b+4）x

∵y1+y2与y1为“同类二次函数”，

∴1+a＞0，得a＞﹣1，

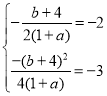
解得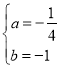或（不符合题意，舍去）

∴y2＝﹣x2﹣x﹣1＝﹣（x﹣2）2，

因为顶点坐标为（2，0），

当﹣3≤x≤0，y2的最大值为0．

答：函数y2的表达式为y2＝﹣x2﹣x﹣1，当﹣3≤x≤0时，y2的最大值为0．