题目内容
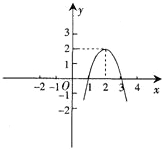
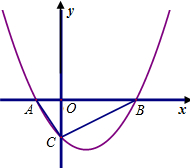
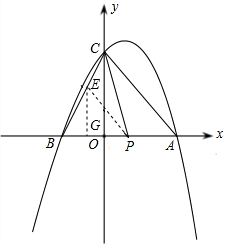
如图,抛物线与x轴交于A(x1,0),B(x2,0)两点,且x1>x2,与y轴交于点C(0,4),其中x1,x2是方程x2-2x-8=0的两个根.
(1)求这条抛物线的解析式;
(2)点P是线段AB上的动点,过点P作PE∥AC,交BC于点E,连接CP,当△CPE的面积最大时,求点P的坐标;
(3)探究:若点Q是抛物线对称轴上的点,是否存在这样的点Q,使△QBC成为等腰三角形?若存在,请直接写出所有符合条件的点Q的坐标;若不存在,请说明理由.

(1)求这条抛物线的解析式;
(2)点P是线段AB上的动点,过点P作PE∥AC,交BC于点E,连接CP,当△CPE的面积最大时,求点P的坐标;
(3)探究:若点Q是抛物线对称轴上的点,是否存在这样的点Q,使△QBC成为等腰三角形?若存在,请直接写出所有符合条件的点Q的坐标;若不存在,请说明理由.

(1)∵x2-2x-8=0,∴(x-4)(x+2)=0.
∴x1=4,x2=-2.
∴A(4,0),B(-2,0).
又∵抛物线经过点A、B、C,设抛物线解析式为y=ax2+bx+c(a≠0),
∴
.
∴
.
∴所求抛物线的解析式为y=-
x2+x+4.
(2)设P点坐标为(m,0),过点E作EG⊥x轴于点G.
∵点B坐标为(-2,0),点A坐标(4,0),
∴AB=6,BP=m+2.
∵PE∥AC,
∴△BPE∽△BAC.
∴
=
.
∴
=
∴EG=
.
∴S△CPE=S△CBP-S△EBP
=
BP•CO-
BP•EG
∴S△CPE=
(m+2)(4-
)
=-
m2+
m+
.
∴S△CPE=-
(m-1)2+3.
又∵-2≤m≤4,
∴当m=1时,S△CPE有最大值3.
此时P点的坐标为(1,0).
(3)存在Q点,
∵BC=2
,
设Q(1,n),
当BQ=CQ时,
则32+n2=12+(n-4)2,
解得:n=1,
即Q1(1,1);
当BC=BQ=2
时,9+n2=20,
解得:n=±
,
∴Q2(1,
),Q3(1,-
);
当BC=CQ=2
时,1+(n-4)2=20,
解得:n=4±
,
∴Q4(1,4+
),Q5(1,4-
).
综上可得:坐标为Q1(1,1),Q2(1,
),Q3(1,-
),Q4(1,4+
),Q5(1,4-
).
∴x1=4,x2=-2.
∴A(4,0),B(-2,0).
又∵抛物线经过点A、B、C,设抛物线解析式为y=ax2+bx+c(a≠0),
∴
|
∴
|
∴所求抛物线的解析式为y=-
| 1 |
| 2 |
(2)设P点坐标为(m,0),过点E作EG⊥x轴于点G.
∵点B坐标为(-2,0),点A坐标(4,0),
∴AB=6,BP=m+2.
∵PE∥AC,
∴△BPE∽△BAC.
∴
| BP |
| AB |
| EG |
| CO |
∴
| EG |
| 4 |
| m+2 |
| 6 |
∴EG=
| 2m+4 |
| 3 |
∴S△CPE=S△CBP-S△EBP
=
| 1 |
| 2 |
| 1 |
| 2 |

∴S△CPE=
| 1 |
| 2 |
| 2m+4 |
| 3 |
=-
| 1 |
| 3 |
| 2 |
| 3 |
| 8 |
| 3 |
∴S△CPE=-
| 1 |
| 3 |
又∵-2≤m≤4,
∴当m=1时,S△CPE有最大值3.
此时P点的坐标为(1,0).
(3)存在Q点,
∵BC=2
| 5 |
设Q(1,n),
当BQ=CQ时,
则32+n2=12+(n-4)2,
解得:n=1,
即Q1(1,1);
当BC=BQ=2
| 5 |
解得:n=±
| 11 |
∴Q2(1,
| 11 |
| 11 |
当BC=CQ=2
| 5 |
解得:n=4±
| 19 |
∴Q4(1,4+
| 19 |
| 19 |
综上可得:坐标为Q1(1,1),Q2(1,
| 11 |
| 11 |
| 19 |
| 19 |


练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目