题目内容
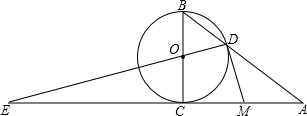 如图,已知Rt△ABC中,∠ACB=90°,BC=6,AB=10,以BC为直径的⊙O交AB于D,AC、DO的延长线交于E,点M为线段AC上一点,且CM=4.
如图,已知Rt△ABC中,∠ACB=90°,BC=6,AB=10,以BC为直径的⊙O交AB于D,AC、DO的延长线交于E,点M为线段AC上一点,且CM=4.(1)求证:直线DM是⊙O的切线;
(2)求ED的长.
考点:切线的判定,相似三角形的判定与性质
专题:代数几何综合题
分析:(1)利用勾股定理得出AC的长,再利用切线的判定定理得出答案;
(2)首先得出△OCE∽△MDE,则
=
=
,进而利用EM2=ED2+DM2,求出ED即可.
(2)首先得出△OCE∽△MDE,则
| OC |
| MD |
| EC |
| ED |
| 3 |
| 4 |
解答: (1)证明:连结CD,
(1)证明:连结CD,
∵Rt△ABC中,∠ACB=90°,BC=6,AB=10,
∴AC=8,
∵CM=4,
∴AM=4,
∴M是AC中点,
∵CD⊥AB,
∴DM=CM=AM,
∠MCD=∠MDC,∠OCD=∠ODC,
∴∠ODM=90°,
∴DM是⊙O的切线;
(2)解:∵DM是⊙O的切线,
∴ED⊥DM,
∴∠ECO=∠EDM,
又∵∠E=∠E,
∴△OCE∽△MDE,
∴
=
=
,
设EC=3x,ED=4x,则EM=3x+4,
EM2=ED2+DM2,
∴(3x+4)2=(4x)2+16,
解得:x=
,
∴ED=4x=
.
 (1)证明:连结CD,
(1)证明:连结CD,∵Rt△ABC中,∠ACB=90°,BC=6,AB=10,
∴AC=8,
∵CM=4,
∴AM=4,
∴M是AC中点,
∵CD⊥AB,
∴DM=CM=AM,
∠MCD=∠MDC,∠OCD=∠ODC,
∴∠ODM=90°,
∴DM是⊙O的切线;
(2)解:∵DM是⊙O的切线,
∴ED⊥DM,
∴∠ECO=∠EDM,
又∵∠E=∠E,
∴△OCE∽△MDE,
∴
| OC |
| MD |
| EC |
| ED |
| 3 |
| 4 |
设EC=3x,ED=4x,则EM=3x+4,
EM2=ED2+DM2,
∴(3x+4)2=(4x)2+16,
解得:x=
| 24 |
| 7 |
∴ED=4x=
| 96 |
| 7 |
点评:此题主要考查了切线的判定以及勾股定理和相似三角形的判定与性质等知识,得出△OCE∽△MDE是解题关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
到△ABC的三个顶点距离相等的点是△ABC( )的交点.
| A、三边中线 |
| B、三条角平分线 |
| C、三边上高 |
| D、三边垂直平分线 |
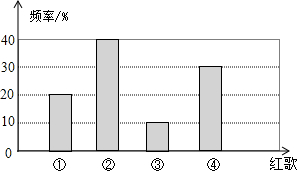 为了筹办“经典红歌唱响金色校园”大合唱,学校选了四首经典红歌:
为了筹办“经典红歌唱响金色校园”大合唱,学校选了四首经典红歌:①《保卫黄河》;②《十送红军》;③《我们走在大路上》;④《我的祖国》.
班长对全班50名同学“你最想唱哪首歌”作了问卷调查,小明将班长的统计结果绘制成如图所示的统计图,并得出以下四个结论,其中错误的是( )
| A、最想唱《十送红军》的人最多 |
| B、最想唱《我的祖国》的人数是最想唱《我们走在大路上》的人数的3倍 |
| C、最想唱《保卫黄河》的人数占全班人数的20% |
| D、有10人对这4首红歌都不想唱 |
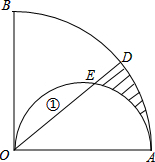 如图,∠BOA=90°,∠AOD=45°,以AO为直径画半圆交OD于E,如果图中①的面积为1cm2,求阴影部分的面积.
如图,∠BOA=90°,∠AOD=45°,以AO为直径画半圆交OD于E,如果图中①的面积为1cm2,求阴影部分的面积.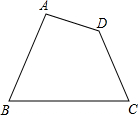 如图为公园的一块草坪,其四角上各有一棵树,现园林工人想使这个草坪的面积扩大一倍,又要四棵树不动,并使扩大后的草坪为平行四边形,试问:这个想法能否实现?若能请你设计出草图?否则请说明理由.
如图为公园的一块草坪,其四角上各有一棵树,现园林工人想使这个草坪的面积扩大一倍,又要四棵树不动,并使扩大后的草坪为平行四边形,试问:这个想法能否实现?若能请你设计出草图?否则请说明理由.