题目内容
⊙A的半径为2厘米,⊙B的半径为3厘米,且圆心所连线段AB的长为6厘米,⊙C与两个圆都相切且半径为6厘米,求符合条件的⊙C的个数.
考点:相切两圆的性质
专题:
分析:由⊙A的半径为2厘米,⊙B的半径为3厘米,且圆心所连线段AB的长为6厘米,可得⊙A与⊙B外离,又由⊙C与两个圆都相切且半径为6厘米,分别从若与两圆都外切,若与两圆都内切,若与⊙A内切,与⊙B外切,若与⊙A外切,与⊙B内切去分析求解即可求得答案.
解答:解:∵⊙A的半径为2厘米,⊙B的半径为3厘米,且圆心所连线段AB的长为6厘米,
∴⊙A与⊙B外离,
∵⊙C与两个圆都相切且半径为6厘米,
∴①若与两圆都外切,则有2个,
②若与两圆都内切,则有1个,
③若与⊙A内切,与⊙B外切,则有2个,
④若与⊙A外切,与⊙B内切,则有2个,
综上可得:符合条件的⊙C的个数有7个.
∴⊙A与⊙B外离,
∵⊙C与两个圆都相切且半径为6厘米,
∴①若与两圆都外切,则有2个,
②若与两圆都内切,则有1个,
③若与⊙A内切,与⊙B外切,则有2个,
④若与⊙A外切,与⊙B内切,则有2个,
综上可得:符合条件的⊙C的个数有7个.
点评:此题考查了相切两圆的性质.此题难度适中,注意掌握分类讨论思想的应用是解此题的关键.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
已知 a=2-2,b=2008°,c=(-1)2011,则a、b、c的大小关系是( )
| A、a>b>c |
| B、b>a>c |
| C、c>a>b |
| D、b>c>a |
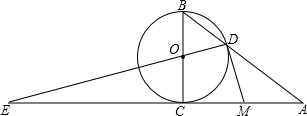 如图,已知Rt△ABC中,∠ACB=90°,BC=6,AB=10,以BC为直径的⊙O交AB于D,AC、DO的延长线交于E,点M为线段AC上一点,且CM=4.
如图,已知Rt△ABC中,∠ACB=90°,BC=6,AB=10,以BC为直径的⊙O交AB于D,AC、DO的延长线交于E,点M为线段AC上一点,且CM=4.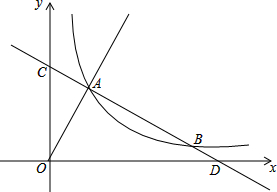 已知直线y=-
已知直线y=- 三条公路围成了一个三角形区域,今要在这个三角形区域内建一果品批发市场到这三条公路的距离相等,试找出批发市场的位置.
三条公路围成了一个三角形区域,今要在这个三角形区域内建一果品批发市场到这三条公路的距离相等,试找出批发市场的位置.