Question

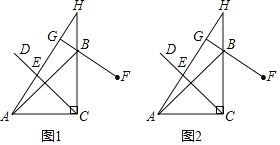
【题目】如图1，在△ABC中，∠ACB＝90°，AC＝BC，E为∠ACB平分线CD上一动点（不与点C重合），点E关于直线BC的对称点为F，连接AE并延长交CB延长线于点H，连接FB并延长交直线AH于点G．

（1）求证：AE＝BF．

（2）用等式表示线段FG，EG与CE的数量关系，并证明．

（3）连接GC，用等式表示线段GE，GC与GF的数量关系是　 　．

Answer 1

【答案】（1）详见解析；（2）结论：FG2+EG2＝2EC2；（3）结论：GE+GF＝CG．

【解析】

（1）连结CF，证明△ACE≌△BCF（SAS）即可解决问题；

（2）结论：FG2+EG2=2EC2，连结EF，通过互补的角和四边形内角和证明∠EGF=90°，再由勾股定理即可解决问题；

（3）结论：GE+GF=CG，证明Rt△CNE≌Rt△CMF（HL），Rt△GCN≌Rt△GCM（HL）即可解决问题．

（1）证明：如图1中，连接CF，

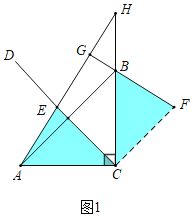
∵CD平分∠ACB，∠ACB=90°，

∴∠ACE=∠BCE=45°，

∵E，F关于CB对称，

∴∠BCF=∠BCE=45°，CE=CF，

∴∠ACE=∠BCF，

在△ACE和△BCF中,

，

∴△ACE≌△BCF（SAS），

∴AE=BF；

（2）解：结论：FG2+EG2=2EC2，

理由：连接EF，CF，

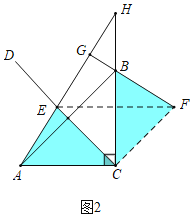
∵△ACE≌△BCF，

∴∠AEC=∠BFC，

∵∠AEC+∠CEG=180°，

∴∠CEG+∠CFG=180°，

∴∠ECF+∠EGF=180°，

∵∠ECB=∠BCF=45°，

∴∠ECF=∠EGF=90°，

∴FG2+EG2=EF2，EF2＝CE2+CF2，

∵CE=CF，

∴FG2+EG2=2CE2，

（3）如图3中，结论：GE+GF=CG，

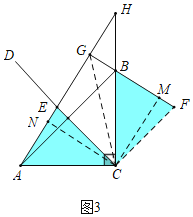
理由：连接CG，CF，作CM⊥BF于F，CN⊥AG于N，

∵△ACE≌△BCF，

∴CN=CM（全等三角形对应边上的高相等），

∵∠CNE=∠CMF=90°，CE=CF，

∴Rt△CNE≌Rt△CMF（HL），

∴EN=FM，

∵∠CNG=∠CMG=90°，CG=CG，

∴Rt△GCN≌Rt△GCM（HL），

∴GN=GM，∠CGN=∠CGM=45°，

∴CG=GN，

∴GE+GF=GNEN+GM+MF=2GN=CG．