题目内容
【题目】若点P为△ABC所在平面上一点,且∠APB=∠BPC=∠CPA=120°,则点P叫做△ABC的费马点.当三角形的最大角小于120°时,可以证明费马点就是“到三角形的三个顶点的距离之和最小的点“.即PA+PB+PC最小.
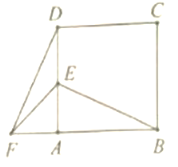
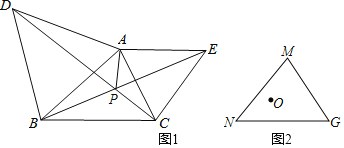
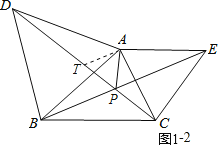
(1)如图1,向△ABC外作等边三角形△ABD,△AEC.连接BE,DC相交于点P,连接AP.
①证明:点P就是△ABC费马点;
②证明:PA+PB+PC=BE=DC;
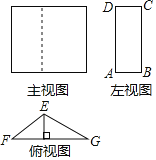
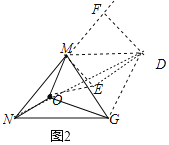
(2)如图2,在△MNG中,MN=4![]() ,∠M=75°,MG=3.点O是△MNG内一点,则点O到△MNG三个顶点的距离和的最小值是 .
,∠M=75°,MG=3.点O是△MNG内一点,则点O到△MNG三个顶点的距离和的最小值是 .
【答案】(1)①证详见解析;②详见解析;(2)![]() .
.
【解析】
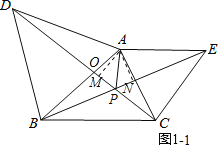
(1)①如图1﹣1中,作AM⊥CD于M,AN⊥BE于N设AB交 CD于O.证明△ADC≌△ABE(SAS)即可解决问题.
②在线段PDA上取一点T,使得PA=PT,连接AT.证明△DAT≌△BAP(SAS),推出PD=PA+PB即可解决问题.
(2)以MG为边作等边三角形△MGD,以OM为边作等边△OME.连接ND,可证△GMO≌△DME,可得GO=DE,则MO+NO+GO=NO+OE+DE,即当D、E、O、N四点共线时,MO+NO+GO值最小,最小值为ND的长度,根据勾股定理先求得MF、DF,然后求ND的长度,即可求MO+NO+GO的最小值.
(1)①如图1﹣1中,作AM⊥CD于M,AN⊥BE于N设AB交 CD于O.
∵△ADB,△ACE都是等边三角形,
∴AD=AB,AC=AE,∠DAB=∠CAE=60°,
∴∠DAB=∠BAE,
∴△ADC≌△ABE(SAS),
∴CD=BE,S△DAC=S△ABE,∠ADC=∠ABE,
∵AM⊥CD,AN⊥BE,
∴![]() CDAM=
CDAM=![]() BEAN,
BEAN,
∴AM=AN,
∴∠APM=∠APN,
∵∠AOD=∠POB,
∴∠OPB=∠DAO=60°,
∴∠APN=∠APM=60°,
∴∠APC=∠BPC=∠APC=120°,
∴点P是就是△ABC费马点.
②在线段PDA上取一点T,使得PA=PT,连接AT.
∵∠APT=60°,PT=PA,
∴△APT是等边三角形,
∴∠PAT=60°,AT=AP,
∵∠DAB=∠TAP=60°,
∴∠DAT=∠BAP,∵AD=AB,
∴△DAT≌△BAP(SAS),
∴PB=DT,
∴PD=DT+PT=PA+PB,
∴PA+PB+PC=PD+PC=CD=BE.
(2)如图2:以MG为边作等边三角形△MGD,以OM为边作等边△OME.连接ND,作DF⊥NM,交NM的延长线于F.
∵△MGD和△OME是等边三角形
∴OE=OM=ME,∠DMG=∠OME=60°,MG=MD,
∴∠GMO=∠DME
在△GMO和△DME中,
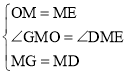 ,
,
∴△GMO≌△DME(
∴OG=DE
∴NO+GO+MO=DE+OE+NO
∴当D、E、O、M四点共线时,NO+GO+MO值最小,
∵∠NMG=75°,∠GMD=60°,
∴∠NMD=135°,
∴∠DMF=45°,
∵MG=3
∴MF=DF=![]() ,
,
∴NF=MN+MF=4![]()
![]() =
=![]() ,
,
∴ND=![]() =
=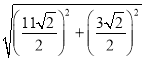 =
=![]() ,
,
∴MO+NO+GO最小值为![]() ,
,
故答案为![]() ,
,

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案