��Ŀ����
����Ŀ����֪����������һ��200�Ļ����ܵ�����ϰ�ܲ������ڰ��ܵ��ֳ���ȵ�4�Σ�������ֱ������������ij�����ͬ����ƽ��ÿ����4�ף���ƽ��ÿ����6�ף����������˷ֱ��A��C����ͬʱ�����������ͼ�����Խ���������⣺
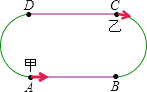
��1������������״���������˵����ʱ�������ܵ��ϵľ���λ�ã�
��2���״��������־�������ʱ�������ٴ�������
��3�����ǵ�100������ʱ������һ���ܵ��ϣ����ڣ�3����ֱ��д�����ۼ��ɣ�
���𰸡���1��10��������״���������ʱ������ֱ��AB�ϣ�����B��40��λ�ã���2��20�룻��3����ʱ����AD�����
��������
��1����ʱ��Ϊx�����ݼ�������·�̺�Ϊ100�г����̣��ⷽ�̼��ɵó��𰸣�
��2����ʱ��Ϊy�����ݼ�������·�̺�Ϊ200�г����̣��ⷽ�̼��ɵó��𰸣�
��3���������100Ȧ���õ�ʱ�䣬�������ʱ���ܵ�Ȧ�������ɵó���.
�⣺��1����x��������״�������
������õ����̣�4x+6x=100
���x=10��
���ܵ�·��=4��10=40�ף�
��10��������״���������ʱ������ֱ��AB�ϣ�����B��40��λ�ã�
��2����y��������ٴ�������������õ����̣�4y+6y=200��
��ã�y=20��
��20��������ٴ�������
��3����һ���������ܹ���ʱ10�룻
�ڶ�������������ʱ10+20��1=30�룻
����������������ʱ10+20��2=50�룻
��
��100������������ʱ10+20��99=1990�룻
��ʱ���ܵ�Ȧ��Ϊ��1990��4��200=39.8
��200��0.8=160
���ʱ����AD����ϣ�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��2019��С��ǰ����µĽ���仯������±���������ʾ��ǰһ�¶��Ǯ����������ʾ��ǰһ���ٵ�Ǯ������λ��Ԫ��
�·� | һ�� | ���� | ���� | ���� | ���� |
Ǯ���仯 |
|
|
|
|
|
��2018��12�·�С�ŵĽ���Ϊ![]() Ԫ.
Ԫ.
��1���ô���ʽ��ʾ2019����·�С�ŵĽ���Ϊ___________Ԫ��
��2��С�����·����ý���ȶ��·ݶ���٣�
����Ŀ��Ϊ�˴������㴫ͳ�Ļ���������֯��һ�γ����꼶1200��ѧ���μӵġ�������д��������Ϊ�˸��õ��˽Ȿ�δ����ijɼ��ֲ�����������ȡ��100��ѧ���ijɼ�������50�֣��������õ����µ�ͳ��ͼ����
�ɼ����֣� | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | ||
�� �� | 1 | 2 | 3 | 3 | 6 | 7 | 5 | 8 | 15 | 9 | 11 | 12 | 8 | 6 | 4 | ||
�ɼ����� | Ƶ�� | Ƶ�� | |||||||||||||||
35��x��38 | 3 | 0.03 | |||||||||||||||
38��x��41 | a | 0.12 | |||||||||||||||
41��x��44 | 20 | 0.20 | |||||||||||||||
44��x��47 | 35 | 0.35 | |||||||||||||||
47��x��50 | 30 | b | |||||||||||||||
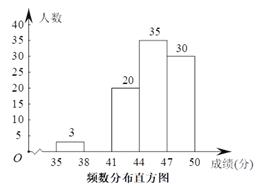
��������ṩ����Ϣ������������
��1����������λ���� �֣�
��2��Ƶ��ͳ�Ʊ���a�� ��b�� ��
��3���벹ȫƵ���ֲ�ֱ��ͼ��
��4������ݳ���ͳ�ƽ�������Ƹôδ����гɼ�������41�ֵ�ѧ���ж�����.