题目内容

将二次函数y=x2-2x-1的图象绕坐标原点O旋转180°，则旋转后的图象对应的解析式为（　　）
A、y=x2+2x+3B、y=-x2-2x+1C、y=x2-2x-1D、y=-x2+2x-3
练习册系列答案
相关题目
如图是二次函数y=ax2+bx+c图象的一部分，其对称轴为x=-1，且过点（-3，0）．下列说法：①abc＜0；②2a-b=0；③4a+2b+c＜0；④3a+c=0；其中说法正确的是（　　）
A、①②B、②③C、①②④D、②③④
抛物线y=x2-3x+2与y轴交点的坐标是（　　）
A、（0，0）B、（2，0）C、（0，2）D、（0，-1）
把抛物线y=x2向下平移2个单位，再向右平移4个单位后得到的抛物线是（　　）
A、y=（x+4）2+2B、y=（x-4）2+2C、y=（x+4）2-2D、y=（x-4）2-2
将抛物线y=5x2向右平移2个单位．再向上平移3个单位．得到的抛物线是（　　）
A、y=5（x+2）2+3B、y=5（x+2）3-3C、y=5（x-2）2+3D、y=5（x-2）2-3
若二次函数y=x2-2x+c的图象与y轴的交点为（0，-3），则此二次函数有（　　）
A、最小值为-2B、最小值为-3C、最小值为-4D、最大值为-4
若关于x的一元二次方程x2+ax+b=0有两个不同的实数根m，n（m＜n），方程x2+ax+b=1有两个不同的实数p，q（p＜q），则m，n，p，q的大小关系为（　　）
A、m＜p＜q＜nB、p＜m＜n＜qC、m＜p＜n＜qD、p＜m＜q＜n
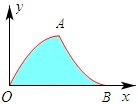曲线y=
-0.5(x-2)2+2，(0≤x≤2)
0.5(x-4)2，(2≤x≤4)
与x轴围成的面积（即图中阴影部分的面积）是多少？下面是课堂教学上同学们的看法，其中最佳答案是（　　）
A、曲线不是圆弧，我们没有学过相关的方法，求不出来
B、既然老师出了这道题，肯定是我们能求出来的，哪个神仙来做
C、我们可以试一试，也许用面积分割的方法能求出来，我猜是4
D、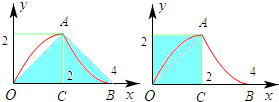
我想出来了，是4；连接OA、OB，作AC⊥OB于C，OC=BC=AC=2，△OAB是等腰直角三角形，又因为分段的两部分对应的二次项系数的绝对值相等，所以这两段抛物线的形状相同，它们自变量的取值长度也相等，都是2，所以分割的部经过剪切，旋转，平移可以填补，就象图中这样，原来的阴影部分面积等于等腰Rt△OAB，也等于那个正方形的面积，是4
如图，△ABC∽△DEF，相似比为1：2．若BC=1，则EF的长是（　　）
A、1B、2C、3D、4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网